题目内容
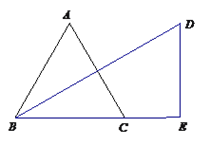
【题目】如图,已知点D为等腰直角△ABC内一点,∠ACB=90°,AD=BD,∠BAD=30°,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM.则下列结论中:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分线AB;④ME=BD;正确的有( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
由等腰三角形的性质可判断①,由“SSS”可证△ADC≌△BDC,可判断②,由全等三角形的性质和等腰三角形的性质可判断③,由“AAS”可证△ACD≌△ECM,可判断④.
解:∵AD=BD,∠BAD=30°,
∴∠BAD=∠ABD=30°,
∴∠ADB=120°,
故①正确;
∵AC=BC,AD=BD,CD=CD,
∴△ADC≌△BDC(SSS),
故②正确;
∵△ADC≌△BDC
∴∠ACD=∠BCD,且AC=BC
∴线段DC所在的直线垂直平分线AB,
故③正确;
∵△ABC是等腰直角三角形,
∴∠CAB=∠CBA,
∴∠CAD=∠CBD=15°,
∵CA=CE,
∴∠E=∠CAD=15°,
∵∠EDC=∠DAC+∠DCA=60°,且CD=CM,
∴∠CDE=∠CMD=60°,
∴∠ADC=∠CME=120°,且∠E=∠CAD,AC=CE,
∴△ACD≌△ECM(AAS),
∴AD=ME=BD,
故④正确,
故选:D.

练习册系列答案
相关题目