题目内容
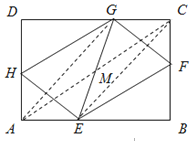
【题目】如图,矩形ABCD中,点E、F、G. H分别AB、BC、 CD、 DA边上的动点,且AE=BF=CG=DH

(1)求证:四边形EFGH是平行四边形:
(2)在点E、F、G、H运动过程中,判断直线GE是否经过某一定点,如果是,请你在图中画出这个点:如果不是,请说明理由.
【答案】(1)证明见解析;(2)是,直线GE总过AC、BD的交点M,作图见解析.
【解析】
(1)由矩形的性质得出∠A=∠C=90°,BC=AD,由AE=BF=CG=DH证出AH=CF,由SAS证明△AEH≌△CGF,可得HE=FG,同理可得HG=FE即可求解;
(2)直线GE经过一个定点,这个定点为矩形的对角线AC、BD的交点.只要证明四边形AECG是平行四边形,即可推出MA=MG,MG=ME,即点M为AC的中点,又矩形ABCD的对角线互相平分,推出点M为矩形对角线ACBD的交点.
解:(1)∵四边形ABCD为矩形,
∴BC=AD,∠A=∠C=90°,
∵BF=DH,
∴BC-BF=AD-DH,即CF=AH,
又AE=CG,
∴△HAE≌△FCG,
∴HE=FG,
同理可证:HG=FE,
∴四边形EFGH是平行四边形.
(2)直线GE经过一个定点,这个定点为矩形的对角线AC、BD的交点.
理由如下:
如图,连结AC、AG、CE,设AC、EG的交点为M.
∵AE∥CG,AE=CG,
∴四边形AECG是平行四边形,
∴MA=MG,MG=ME,
即点M为AC的中点,
又矩形ABCD的对角线互相平分
∴点M为矩形对角线ACBD的交点,
∴直线GE总过AC、BD的交点M.

练习册系列答案
相关题目








