题目内容
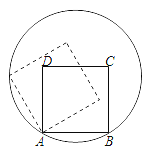
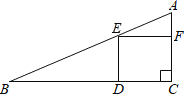
【题目】如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
【答案】A
【解析】
设AF=x,根据正方形的性质用x表示出EF、CF,证明△AEF∽△ABC,根据相似三角形的性质求出BC,根据勾股定理列式求出x,根据三角形的面积公式、正方形的面积公式计算即可.
设AF=x,则AC=3x,FC=2x,
∵四边形CDEF为正方形,
∴EF=CF=2x,EF∥BC,
∴△AEF∽△ABC,
∴![]() ,
,
∴BC=6x,
在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,
解得,x=2![]() ,
,
∴AC=6![]() ,BC=12
,BC=12![]() ,
,
∴剩余部分的面积=![]() ×12
×12![]() ×6
×6![]() ﹣4
﹣4![]() ×4
×4![]() =100(cm2),
=100(cm2),
故选A.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
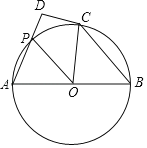
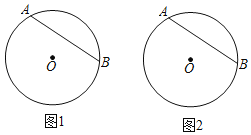
第三学期赢在暑假系列答案【题目】在⊙O中,![]() 的度数为120°,点P为弦AB上的一点,连结OP并延长交⊙O于点C,连结OB,AC.
的度数为120°,点P为弦AB上的一点,连结OP并延长交⊙O于点C,连结OB,AC.
(1)若P为AB中点,且PC=1,求圆的半径.
(2)若BP:BA=1:3,请求出tan∠OPA.
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值