题目内容
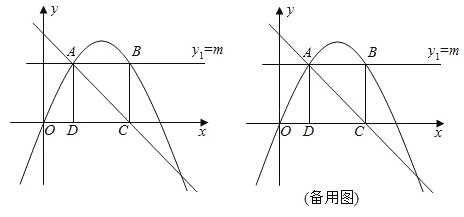
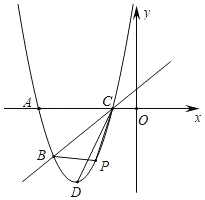
【题目】如图，已知抛物线y＝ax2+bx+5经过A(﹣5，0)，B(﹣4，﹣3)两点，与x轴的另一个交点为C，顶点为D，连结CD．
(1)求该抛物线的表达式；
(2)点P为该抛物线上一动点(与点B、C不重合)，设点P的横坐标为t．
①当点P在直线BC的下方运动时，求△PBC的面积的最大值；
②该抛物线上是否存在点P，使得∠PBC＝∠BCD？若存在，求出所有点P的坐标；若不存在，请说明理由．
【答案】(1)y＝x2+6x+5；(2)①S△PBC的最大值为
；②存在，点P的坐标为P(﹣
，﹣
)或(0，5)．
【解析】
(1)将点A、B坐标代入二次函数表达式，即可求出二次函数解析式；
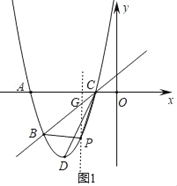
(2)①如图1，过点P作y轴的平行线交BC于点G，将点B、C的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝x+1，设点G(t，t+1)，则点P(t，t2+6t+5)，利用三角形面积公式求出最大值即可；
②设直线BP与CD交于点H，当点P在直线BC下方时，求出线段BC的中点坐标为(﹣
，﹣
)，过该点与BC垂直的直线的k值为﹣1，求出 直线BC中垂线的表达式为：y＝﹣x﹣4…③，同理直线CD的表达式为：y＝2x+2…④，、联立③④并解得：x＝﹣2，即点H(﹣2，﹣2)，同理可得直线BH的表达式为：y＝
x﹣1…⑤，联立⑤和y＝x2+6x+5并解得：x＝﹣，即可求出P点；当点P(P′)在直线BC上方时，根据∠PBC＝∠BCD求出BP′∥CD，求出直线BP′的表达式为：y＝2x+5，联立y＝x2+6x+5和y＝2x+5，求出x，即可求出P.
解：(1)将点A、B坐标代入二次函数表达式得：
，
解得：
，
故抛物线的表达式为：y＝x2+6x+5…①，
令y＝0，则x＝﹣1或﹣5，
即点C(﹣1，0)；
(2)①如图1，过点P作y轴的平行线交BC于点G，
将点B、C的坐标代入一次函数表达式并解得：
直线BC的表达式为：y＝x+1…②，
设点G(t，t+1)，则点P(t，t2+6t+5)，
S△PBC＝PG(xC﹣xB)＝(t+1﹣t2﹣6t﹣5)＝﹣t2﹣
t﹣6，
∵-＜0，
∴S△PBC有最大值，当t＝﹣时，其最大值为
；
②设直线BP与CD交于点H，
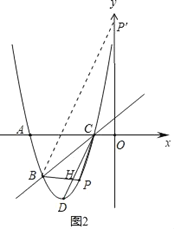
当点P在直线BC下方时，
∵∠PBC＝∠BCD，
∴点H在BC的中垂线上，
线段BC的中点坐标为(﹣，﹣)，
过该点与BC垂直的直线的k值为﹣1，
设BC中垂线的表达式为：y＝﹣x+m，将点(﹣，﹣)代入上式并解得：
直线BC中垂线的表达式为：y＝﹣x﹣4…③，
同理直线CD的表达式为：y＝2x+2…④，
联立③④并解得：x＝﹣2，即点H(﹣2，﹣2)，
同理可得直线BH的表达式为：y＝x﹣1…⑤，
联立①⑤并解得：x＝﹣或﹣4(舍去﹣4)，
故点P(﹣，﹣
)；
当点P(P′)在直线BC上方时，
∵∠PBC＝∠BCD，∴BP′∥CD，
则直线BP′的表达式为：y＝2x+s，将点B坐标代入上式并解得：s＝5，
即直线BP′的表达式为：y＝2x+5…⑥，
联立①⑥并解得：x＝0或﹣4(舍去﹣4)，
故点P(0，5)；
故点P的坐标为P(﹣，﹣)或(0，5)．
阅读快车系列答案【题目】为了提高学生的汉字书写能力，某学校连续举办了几届汉字听写大赛，今年经过层层选拔，确定了参加决赛的选手，决赛的比赛规则是每正确听写出1个汉字得2分，满分是100分，下面是根据决赛的成绩绘制出的不完整的频数分布表、扇形统计图和频数分布直方图．
类别 | 成绩x分 | 频数（人数） |
A | 50≤x＜60 | 5 |
B | 60≤x＜70 | 7 |
C | 70≤x＜80 | a |
D | 80≤x＜90 | 15 |
E | 90≤x＜100 | 10 |
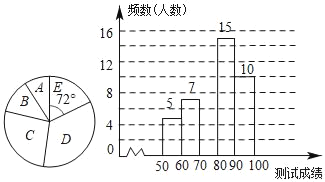
请结合图表完成下列各题
（1）表中a的值为 ，并把频数分布直方图补充完整；
（2）学校想利用频数分布表估计这次决赛的平均成绩，谐你直接写出平均成绩；
（3）通过与去年的决赛成绩进行比较，发现今年各类人数的中位数有了显著提高，提高了15%以上，求去年各类人数的中位数最高可能是多少？
（4）想从A类学生的3名女生和2名男生中选出两人进行培训，直接写出选中1名男生和1名女生的概率是多少．
