��Ŀ����
��ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1����ABC��ƽ��ֱ������ϵ�е�λ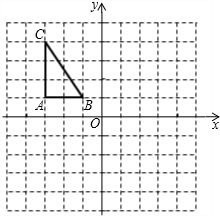 ����ͼ��ʾ��
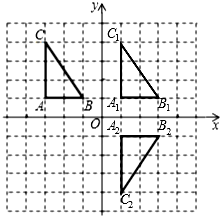
����ͼ��ʾ����1������ABC����ƽ��4����λ�õ���A1B1C1���뻭����A1B1C1����ֱ��д����C1�����꣮
��2��������A1B1C1����x��ĶԳ�ͼ�Ρ�A2B2C2����ֱ��д����A2�����꣮
��3������ͼ��ֱ���ж��Ե�C1��C2��B2��B1Ϊ������ı�����ʲô�ı��Σ���������������
��������1���ѡ�ABC�ĸ�����������ƽ��4����λ��˳�����Ӽ��ɣ�
��2���õ���A1B1C�ĸ�������1����x��ĶԳƵ㣬˳�����ӣ�����A2������������������ľ���ɵ���Ӧ���ꣻ
��3����Ϊ���Σ���������������㼴�ɣ�
��2���õ���A1B1C�ĸ�������1����x��ĶԳƵ㣬˳�����ӣ�����A2������������������ľ���ɵ���Ӧ���ꣻ
��3����Ϊ���Σ���������������㼴�ɣ�
��� ����������6�֣�
����������6�֣�
�⣺��1����ȷ��������ƽ��4����λ��ͼ�Σ���1�֣�
C1��1��4����1�֣�
��2����ȷ����ͼ�Σ���1�֣�
A2��1��-1������1�֣�
��3���ı���C1C2B2B1�ǵ������Σ���1�֣�
��ͼ�ɵã�B1B2=2��C1C2=8��A1B1=2��
��������=
=
=10��1�֣���
 ����������6�֣�
����������6�֣��⣺��1����ȷ��������ƽ��4����λ��ͼ�Σ���1�֣�
C1��1��4����1�֣�
��2����ȷ����ͼ�Σ���1�֣�
A2��1��-1������1�֣�
��3���ı���C1C2B2B1�ǵ������Σ���1�֣�
��ͼ�ɵã�B1B2=2��C1C2=8��A1B1=2��
��������=
| (B1B2+C1C2)��A1B1 |
| 2 |
| (8+2)��2 |
| 2 |
�������ۺϿ���ƽ����ͼ���Գ���ͼ��ע��ͼ�εı任�����ؼ���ı任���ɣ�

��ϰ��ϵ�д�
�����Ŀ
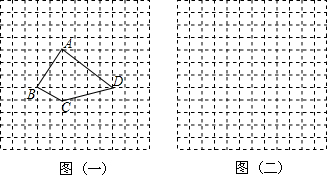
 ��ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1��
��ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1��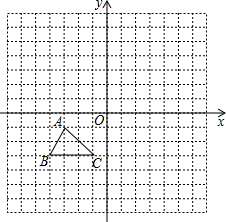 ϵ��ABC�Ķ����ڸ���ϣ���B������Ϊ��-4��-3����
ϵ��ABC�Ķ����ڸ���ϣ���B������Ϊ��-4��-3����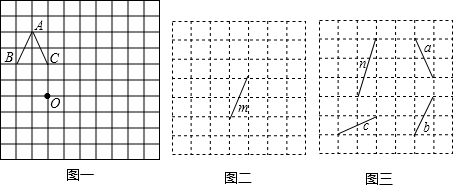
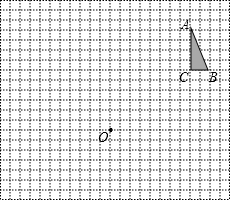
 ��ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1����ABC�͵�S��λ����ͼ��ʾ��
��ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1����ABC�͵�S��λ����ͼ��ʾ��