题目内容
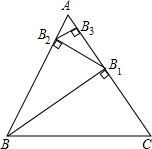 如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,B3B4是△AB2B3的高,…Bn-1Bn是△ABn-2Bn-1的高
如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,B3B4是△AB2B3的高,…Bn-1Bn是△ABn-2Bn-1的高(1)求BB1的长;
(2)填空:B1B2的长为
(3)根据(1)、(2)的计算结果,猜想写出Bn-1Bn的值(用含n的代数式表示,n为正整数).
分析:本题要根据等边三角形的性质、勾股定理的多次运用求解,再根据规律推出Bn-1Bn的值.
解答:解:(1)∵△ABC是一个边长为1的等边三角形,BB1是△ABC的高
∴BC=1,B1C=
∵在直角三角形BB1C中
BC2=BB12+B1C2
∴BB1=
=
=
;
(2)∵△ABC是一个边长为1的等边三角形,BB1是△ABC的高
∴AB1=
∵B1B2是△ABB1的高
∴
×B1B2×AB=
×AB1×BB1
∵BB1=
∴B1B2=
.
同理可得B2B3=
.
(3)猜想:Bn-1Bn=
.
∴BC=1,B1C=
| 1 |
| 2 |
∵在直角三角形BB1C中
BC2=BB12+B1C2
∴BB1=
| BC2-B1C2 |
12-(
|
| ||
| 2 |
(2)∵△ABC是一个边长为1的等边三角形,BB1是△ABC的高
∴AB1=
| 1 |
| 2 |
∵B1B2是△ABB1的高
∴
| 1 |
| 2 |
| 1 |
| 2 |
∵BB1=
| ||
| 2 |
∴B1B2=
| ||
| 4 |
同理可得B2B3=
| ||
| 8 |
(3)猜想:Bn-1Bn=
| ||
| 2n |
点评:本题是开放性试题,要求具备较强的逻辑推理能力.

练习册系列答案
相关题目
 2、如图,△ABC是一个等边三角形,它绕着点P旋转,可以与等边△ABD重合,则这样的点P有
2、如图,△ABC是一个等边三角形,它绕着点P旋转,可以与等边△ABD重合,则这样的点P有 如图,△ABC是一个圆锥的左视图,其中AB=AC=5,BC=8,则这个圆锥的侧面积是
如图,△ABC是一个圆锥的左视图,其中AB=AC=5,BC=8,则这个圆锥的侧面积是 如图,△ABC是一个等腰三角形,直角边的长度是1米,现在以点C为圆心,把三角形ABC顺时针旋转90度,那么,AB边在旋转时所扫过的面积是( )平方米.
如图,△ABC是一个等腰三角形,直角边的长度是1米,现在以点C为圆心,把三角形ABC顺时针旋转90度,那么,AB边在旋转时所扫过的面积是( )平方米.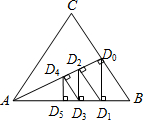 (2013•怀柔区一模)如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;…;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,…,则线段D1D2的长为
(2013•怀柔区一模)如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;…;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,…,则线段D1D2的长为