题目内容
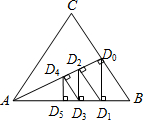 (2013•怀柔区一模)如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;…;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,…,则线段D1D2的长为
(2013•怀柔区一模)如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;…;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,…,则线段D1D2的长为| 3 |
| 4 |
| 3 |
| 4 |
(
)n
| ||
| 2 |
(
)n
(n为正整数).
| ||
| 2 |
分析:由三角形ABC为等边三角形,AD0⊥BC,利用等边三角形的性质及三线合一得到BD0=1,∠B=60°,再由D0D1⊥AB,得到∠D1D0B=30°,利用锐角三角函数定义求出D1D0的长,同理求出D1D2的长,依此类推得出Dn-1Dn的长.
解答:解:∵△ABC是一个边长为2的等边三角形,AD0⊥BC,
∴BD0=1,∠B=60°,
∵D0D1⊥AB,
∴∠D1D0B=30°,
∴D1D0=BD0cos∠D1D0B=
,
同理∠D0D1D2=30°,D1D2=D1D0cos∠D0D1D2=(
)2=
,
依此类推,线段Dn-1Dn的长为(
)n.
故答案为:
;(
)n
∴BD0=1,∠B=60°,
∵D0D1⊥AB,
∴∠D1D0B=30°,
∴D1D0=BD0cos∠D1D0B=
| ||
| 2 |
同理∠D0D1D2=30°,D1D2=D1D0cos∠D0D1D2=(
| ||
| 2 |
| 3 |
| 4 |
依此类推,线段Dn-1Dn的长为(
| ||
| 2 |
故答案为:
| 3 |
| 4 |
| ||
| 2 |
点评:此题考查了等边三角形的性质,锐角三角函数定义,属于规律型试题,弄清题中的规律是解本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 (2013•怀柔区一模)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(2013•怀柔区一模)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB. (2013•怀柔区一模)如图,已知直线AB∥CD,∠C=125°,∠A=45°,则∠E的度数为
(2013•怀柔区一模)如图,已知直线AB∥CD,∠C=125°,∠A=45°,则∠E的度数为