题目内容
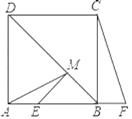
【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ).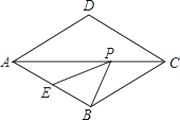
A.1
B.2
C.![]()
D.![]()
【答案】D
【解析】解:如图所示,作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,
∵菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,
∴AE′=AE=BE=1,
∴△AEE′为等边三角形,
∴∠AEE′=60°,
∴∠E′EB=120°,
∵BE=EE′,
∴∠EE′B=30°,
∴∠AE′B=90°,
BE′= ![]() ,
,
∵PE+PB=BE′,
∴PE+PB的最小值是: ![]() .
.
故答案为: ![]() .作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,由菱形性质和题意可得AE′=AE=BE=1,根据等边三角形判定即可知△AEE′为等边三角形,由等边三角形性质可得∠AEE′=60°,由邻补角定义得∠E′EB=120°,根据等腰三角形性质和三角形内角和得∠AE′B=90°,根据勾股定理即可得
.作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,由菱形性质和题意可得AE′=AE=BE=1,根据等边三角形判定即可知△AEE′为等边三角形,由等边三角形性质可得∠AEE′=60°,由邻补角定义得∠E′EB=120°,根据等腰三角形性质和三角形内角和得∠AE′B=90°,根据勾股定理即可得
BE′=![]() ,由PE+PB=BE′即可得出答案.
,由PE+PB=BE′即可得出答案.

练习册系列答案
相关题目
【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.