题目内容
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.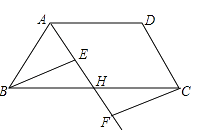
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
【答案】
(1)解:添加条件:EH=FH,
∵点H是BC的中点,
∴BH=CH,
在△BEH和△CFH中, ,
,
∴△BEH≌△CFH(SAS).
(2)解:当BH=EH时,四边形BFCE是矩形,理由如下:
∵BH=CH,EH=FH,
∴四边形BFCE是平行四边形(对角线互相平分的四边形为平行四边形),
∵当BH=EH时,
∴BC=EF,
∴平行四边形BFCE为矩形(对角线相等的平行四边形为矩形)
【解析】(1)解:添加条件:EH=FH;根据中点定义得BH=CH,再根据全等三角形判定SAS得△BEH≌△CFH.
(2)当BH=EH时,四边形BFCE是矩形,理由如下:根据对角线互相平分的四边形为平行四边形得四边形BFCE是平行四边形;再根据对角线相等的平行四边形为矩形得平行四边形BFCE为矩形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目