题目内容
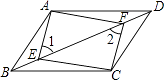
【题目】如图，四边形ABCD中，AB＝CD，AB∥CD，点E、F在线段BD上，且BE＝DF，连接AE、CF．
（1）指出线段AE与CF的关系，并说明理由；
（2）若将题中的条件“点E、F在线段BD上”改为“点E、F在直线BD上” ，那么(1)中的结论还一定能成立吗？若能，直接写出结论；若不能，请举出反例加以说明．
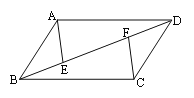
【答案】（1）AE∥CF，AE＝CF（2）不一定成立
【解析】
（1）由SAS证明△ABE≌△CDF，即可得出结论；
（2）画出图形，即可得出结论．
解：(1) AE∥CF，AE＝CF 理由如下：
∵AB∥CD，∴∠ABE＝∠CDF．
在△ABE和△CDF中，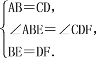
∴△ABE≌△CDF．
∴AE＝CF，∠AEB＝∠CFD．
∴∠AED ＝ ∠CFB，
∴AE∥CF
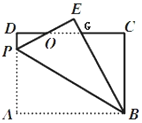
(2)不一定成立；如图所示，AE与CF不平行，AE≠CF．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
