题目内容
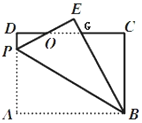
【题目】如图, 矩形ABCD中,AB=8,BC=6,P为AD上一点, 将△ABP 沿BP翻折至△EBP, PE与CD相交于点O,BE与DC相交于G点,且OE=OD,
(1)求证:AP=DG
(2)若设AP=x,则GE=______,GC=_______(用含有x的代数式表示);并求AP的长度
【答案】(1)见详解;(2)6-x; 8-x;AP=4.8 .
【解析】
(1)先根据长方形的性质证得△BAP≌△BEP,得到AP=EP,再证明△ODP≌△OEG,进而得到DG=EP,即可证明AP=DG;(2)由△ODP≌△OEG可得GE=DP=6-x,由AP=DG得到GC=8-x,最后根据勾股定理求出AP的长即可.
(1)∵四边形ABCD是长方形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.
根据题意得△BAP≌△BEP,
∴AP=EP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,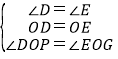 ,
,
∴△ODP≌△OEG,
∴OP=OG,PD=GE,
∴DG=EP,
∴AP=DG.
(2))由(1)易知GE=DP=6-x,DG=x,
∴GC=8-x,BG=8-(6-x)=2+x,
根据勾股定理得到BC2=GC2+BG2,即62+(8-x)2=(x+2)2,
解得x=4.8,
∴AP=4.8.

【题目】某商店购进某种茶壶、茶杯共200个进行销售,其中茶杯的数量是茶壶数量的5倍还多20个.销售方式有两种:(1)单个销售;(2)成套销售.相关信息如下表:
进价(元/个) | 单个售价(元/个) | 成套售价(元/套) | |
茶壶 | 24 | a | 55 |
茶杯 | 4 | a﹣30 | |
备注:(1)一个茶壶和和四个茶杯配成一套(如图); (2)利润=(售价﹣进价)×数量 | |||
(1)该商店购进茶壶和茶杯各有多少个?
(2)已知甲顾客花180元购买的茶壶数量与乙顾客花30元购买的茶杯数量相同.
①求表中a的值.
②当该商店还剩下20个茶壶和100个茶杯时,商店将这些茶壶和茶杯中的一部分按成套销售,其余按单个销售,这120个茶壶和茶杯全部售出后所得的利润为365元.问成套销售了多少套?