题目内容
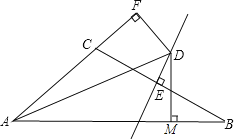
【题目】如图,点A的坐标为(0,2),点B为一、三象限角平分线上的一个动点,BC⊥AB交x轴的正半轴于点C.当∠OAB=_____°时,△COB是等腰三角形.

【答案】90或112.5
【解析】
先依据点B在一、三象限角平分线上求得∠AOB=∠BOC=45°,然后再分为∠BOC=∠OBC和∠OCB=∠BCO、∠BOC=∠BCO三种情况求解即可.
解:∵点B在一、三象限角平分线上,
∴∠BOC=45°.
当∠BOC=∠OBC时,∠BOC=∠OBC=45°,
∴BC⊥OC,
∴∠BCO=90°.
又∵BC⊥AB,
∴AB⊥OA,
∴∠OAB=90°.
当∠CBO=∠BCO时,∠CBO=67.5°,
∵BC⊥AB,
∴∠CBA=90°,
∴∠ABO=90°﹣67.5°=22.5°.
∴∠OAB=180°﹣∠AOB﹣∠ABO=112.5°.
当∠BOC=∠BCO时,∠CBO=90°,则AB∥OB,
∴此种情况不存在.
故答案为:90°或112.5°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目