Question

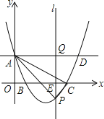
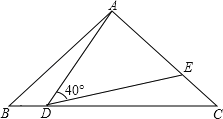
【题目】如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E点．

（1）当∠BDA=115°时，∠BAD=___°，∠DEC=___°；

（2）当DC等于多少时，△ABD与△DCE全等？请说明理由；

（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数；若不可以，请说明理由．

Answer 1

【答案】（1） 25，115；（2）当DC=2时，△ABD≌△DCE，理由见解析；（3）可以；当∠BDA的度数为110°或80°时，△ADE的形状是等腰三角形．

【解析】

（1）根据三角形内角和定理，将已知数值代入即可求出，根据平角的定义，可求出的度数，根据三角形内和定理，即可求出．

（2）当时，利用可证明，即可得出．

（3）假设是等腰三角形，分为三种情况讨论：①当时，，根据，得出此时不符合；②当时，求出，求出，根据三角形的内角和定理求出，根据三角形的内角和定理求出即可；③当时，求出，求出，根据三角形的内角和定理求出．

（1）在中， ，，，．

，，，．

故答案为：，；

（2）当时，．理由如下：

，，又，，．

在和中，，，当时，，；

（3），，分三种情况讨论：

①当时，，，此时不符合；

②当时，即，，；

；

③当时，，，；

当或时，是等腰三角形．