题目内容
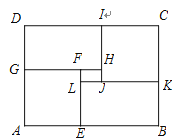
【题目】在矩形ABCD中，AB=8，BC=6，将矩形按图示方式进行分割，其中正方形AEFG与正方形JKCI全等，矩形GHID与矩形EBKL全等．
（1）当矩形LJHF的面积为
时，求AG的长；
（2）当AG为何值时，矩形LJHF的面积最大．
【答案】（1）
或
；（2）
.
【解析】试题分析： 
设AG=x，DG=6-x ，BE=8-x，FL=x-(6-x)=2x-6，LJ=8-2x，
矩形
，即可求出
的长度.
设矩形LJHF的面积为S，根据配方法求出面积的最大值.
试题解析：（1）
正方形AEFG和正方形JKCI全等，矩形GHID和矩形EBKL全等，
设AG=x，DG=6-x ，BE=8-x，FL=x-(6-x)=2x-6，LJ=8-2x，
方法1： 
矩形
，
∴
，
∴
， 
AG=
或AG=
．
方法2： 
S矩形LIHF=S矩形ABCD-2S矩形DGHI-2S正方形AEFG.
，
∴
， 
AG=
或AG=
．
（2）设矩形LJHF的面积为S，
，
.
,
，
S有最大值，
当AG=
时，矩形LJHF的面积最大．
练习册系列答案
相关题目
【题目】某公司有A、B两种型号的客车，它们的载客量、每天的租金如表所示：
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
已知某中学计划租用A、B两种型号的客车共10辆，同时送七年级师生到沙家参加社会实践活动，已知该中学租车的总费用不超过5600元．
(1)求最多能租用多少辆A型号客车？
(2)若七年级的师生共有380人，请写出所有可能的租车方案．
