��Ŀ����
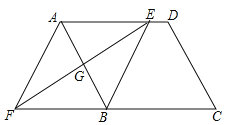
����Ŀ����ͼ���ڡ�ABC�У�AC��BC��2����C��90������һ��������ǰ��ֱ�Ƕ������б��AB���е�P���������ǰ��Ƶ�P��ת�����ǰ����ֱ�DZ߷ֱ�����AC��CB��D��E���㣮��ͼ�١��ڡ�������ת���ǰ�õ���ͼ���е�3��������о���
��1�����ǰ��Ƶ�P��ת���۲��߶�PD��PE֮����ʲô������ϵ�����ͼ��˵�����ɣ�
��2�����ǰ��Ƶ�P��ת����PCE�Ƿ��ܳ�Ϊ���������Σ����ܣ�ָ�����������ֱ��д�𰸣���
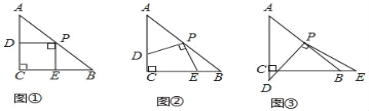
���𰸡���1��PD=PE,֤������������2����PCE�ܳ�Ϊ���������Σ�֤��������
��������
��1��PD=PE��ͨ��֤��DPC�ա�EPB���ɵý���
��2��������������ۢٵ�PC��PE��![]() ʱ���ڵ�PC��CE��
ʱ���ڵ�PC��CE��![]() ʱ���۵�PE��ECʱ������⣮
ʱ���۵�PE��ECʱ������⣮
��:��1��PD=PE���������£�
��D��AC��ʱ������PC��

��Ϊ��ABC�ǵ���ֱ�������Σ�P��AB���е㣬
��CP=PB��CP��AB����ACP=![]() ��ACB=45����
��ACB=45����
���ACP=��B=45����
�֡ߡ�DPC+��CPE=��BPE+��CPE��
���DPC=��BPE��
���PCD�ա�PBE��
��PD=PE��
��D��AC��ʱ������PC��

��Ϊ��ABC�ǵ���ֱ�������Σ�P��AB���е㣬
��CP=PB��CP��AB����ACP=![]() ��ACB=45����
��ACB=45����
���ACP=��CBP=45����
���PCD=��PBE=135����
�֡ߡ�DPC+��DPB=��DPB+��BPE��
���DPC=��BPE��
���PCD�ա�PBE��
��PD=PE
����������PD=PE��
��2����PBE�ǵ��������Σ��������£�
��AC��BC��2����C��90��
��AB��2![]()
��AP��BP��CP��![]()
��PCE�ǵ���������
��PC��PE��![]() ʱ����B��E�غϣ�BE��0
ʱ����B��E�غϣ�BE��0
��PC��CE��![]() ʱ����E���߶�BC�ϣ���BE��2��
ʱ����E���߶�BC�ϣ���BE��2��![]()
��PC��CE��![]() ʱ����E���߶�BC���ӳ����ϣ���BE��2+
ʱ����E���߶�BC���ӳ����ϣ���BE��2+![]()
��PE��EC���ҡ�PCB��45��
���PEC��90��
��EC��1
��BE��1

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�