题目内容
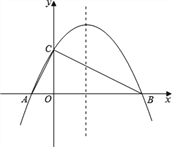
【题目】如图，已知抛物线
与x轴相交于A、B两点，与y轴相交于点C（0,4），若已知A点的坐标为A（﹣2，0）．
（1）求抛物线的解析式；
（2）求△ABC的外接圆圆心坐标；
（3）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标,若不存在，请说明理由．
【答案】(1)
;(2) 圆心坐标为（3,0）;(3)见解析.
【解析】分析：
（1）将A、C两点的坐标代入抛物线的解析式列出关于b、c的方程组，解方程组求得b、c的值即可得到所求解析式；
（2）由（1）中所得解析式先求出点B的坐标，再结合点A、C的坐标求得线段AC、BC、AB的长，由勾股定理的逆定理证得∠ACB=90°，由此即可得到△ABC的外心是斜边AB的中点，由此即可得到所求坐标；
（3）由（1）中所得抛物线的解析式可求得抛物线的对称轴为直线x=3，设点Q的坐标为（3，t），结合点A、C的坐标可将AC、AQ和CQ的长度表达出来，然后分AQ=CQ、AC=CQ和AQ=AC三种情况列出方程，解方程即可求得符合条件的点Q的坐标.
详解：
（1）∵抛物线
的图象经过点A（﹣2，0），C（0,4）
∴ 
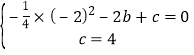
解得：b=
，c=4
∴抛物线解析式为
；
（2）在中，令y=0，即
，
整理得x2﹣6x﹣16=0，解得：x=8或x=﹣2，
∴A（﹣2，0），B（8，0），
∴OA=2，OC=4，OB=8，AB=10，
∴
，
∴
∴△ABC是直角三角形，且
，
∴△ABC的外接圆圆心在AB边上的中点处，圆心坐标为（3，0），
（3）∵
，
∴抛物线的线的对称轴为：x=3，
可设点Q（3，t），∵点A、C的坐标分别为（-2，0）和（0，4），
∴AC=
，AQ=
，CQ=
，
i）当AQ=CQ时，
有
，即25+t2=t2﹣8t+16+9，
解得t=0，
∴Q1（3，0）；
ii）当AC=AQ时，
有
，即
，此方程无实数根，
∴此时△ACQ不能构成等腰三角形；
iii）当AC=CQ时，
有
，即：t2﹣8t+5=0，
解得：t=4±
，
∴点Q坐标为：Q2（3，4+），Q3（3，4﹣）．
综上所述，存在点Q，使△ACQ为等腰三角形，点Q的坐标为：Q1（3，0），Q2（3，4+），Q3（3，4﹣）.
