Question

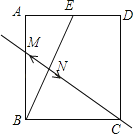
【题目】如图，矩形纸片ABCD中，点E是AD的中点，且AE＝1，连接BE，分别以B、E为圆心，以大于的长为半径作弧，两弧交于点M、N，若直线MN恰好过点C，则AB的长度为（　　）

A.B.C.D.2

Answer 1

【答案】B

【解析】

如图，连接EC，记MN与BE的交点为F，由FC垂直平分BE，得到∠BFC=∠EFC=90°，EF=BF，由于FC=FC，推出△BFC≌△CEF（SAS），于是得到BC=EC利用勾股定理可得答案．

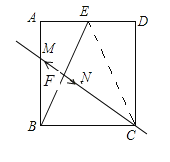
解：如图，连接EC ，记MN与BE的交点为F，

∵FC垂直平分BE，

即∠BFC=∠EFC=90°，EF=BF，

又∵FC=FC，

在△BFC与△CEF中

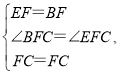
∴△BFC≌△EFC（SAS），

∴BC=EC

又∵AD=BC，AE=1，为AD的中点，

EC=2 ，

由勾股定理得：AB=CD＝

故选：B．