题目内容
在四边形ABCD中,已知△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则边CD的长为______.
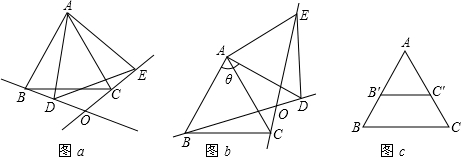
如图,以CD为边作等边△CDE,连接AE.
∴CD=CE=DE,∠DCE=∠CDE=60°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵∠BCD=∠BCA+∠ACD,∠ACE=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
∵
,
∴△BCD≌△ACE(SAS),
∴AE=BD=5.
又∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=90°.
在Rt△ADE中,AE=5,AD=3,
∴DE=
=4,
∴CD=DE=4.
故答案为:4.

∴CD=CE=DE,∠DCE=∠CDE=60°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵∠BCD=∠BCA+∠ACD,∠ACE=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
∵
|
∴△BCD≌△ACE(SAS),
∴AE=BD=5.
又∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=90°.
在Rt△ADE中,AE=5,AD=3,
∴DE=
| AE2-AD2 |
∴CD=DE=4.
故答案为:4.


练习册系列答案
相关题目


 -5,-4),C(-5,-1)
-5,-4),C(-5,-1)
