题目内容
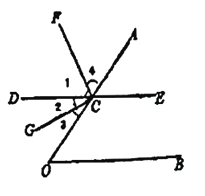
【题目】推理填空:如图,点![]() 在
在![]() 的一边
的一边![]() 上,过点
上,过点![]() 的直线
的直线![]() 平行直线
平行直线![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)当![]() 为多少度时,
为多少度时,![]() 平分
平分![]() ,并说明理由。
,并说明理由。
(1)证明:∵![]() (已知)
(已知)
∴![]() (垂直定义)
(垂直定义)
即![]()
又∵![]() (平角定义)
(平角定义)
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() (角平分线定义)
(角平分线定义)
∴![]() (_____________________)
(_____________________)
即![]() 平分
平分![]() ;
;
(2)解:![]() 时,
时,![]() 平分
平分![]() ,理由如下:
,理由如下:
∵![]() ,
,
∴![]() (____________________________),
(____________________________),
∴![]() _________________°
_________________°
又∵![]() 平分
平分![]() ,
,
∴![]() °,
°,
∴![]() (等量代换)
(等量代换)
即![]() 平分
平分![]() .
.
【答案】(1)详见解析;(2)![]() 时,
时,![]() 平分
平分![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)由CG与CF垂直,利用垂直的定义得到一个直角,再由CF为角平分线,利用等角的余角相等即可得证;
(2)当∠O为60度时,CD平分∠OCF,由平行线的性质及角平分线定义验证即可.
(1)证明:∵![]() (已知)
(已知)
∴![]() (垂直定义)
(垂直定义)
即![]() ,
,
又∵![]() (平角定义)
(平角定义)
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() (角平分线定义),
(角平分线定义),
∴![]() (等角的余角相等)
(等角的余角相等)
即![]() 平分
平分![]() ;
;
(2)解:![]() 时,
时,![]() 平分
平分![]() ,理由如下:
,理由如下:
∵![]() ,
,
∴![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
∴![]() ,
,
又∵![]() 平分
平分![]() ,
,
∴![]()
∴![]() (等量代换)
(等量代换)
即![]() 平分
平分![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目