题目内容
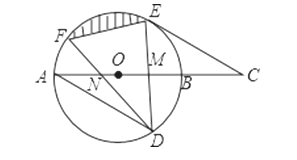
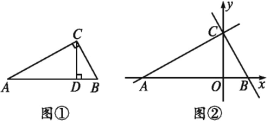
【题目】如图,在![]() 中,
中,![]() ,将
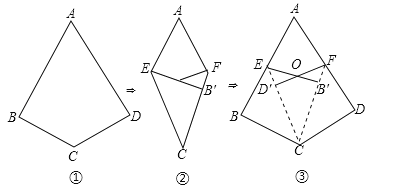
,将![]() 绕点
绕点![]() 逆时针方向旋转得到
逆时针方向旋转得到![]() ,当点
,当点![]() 落在
落在![]() 边上时,
边上时,![]() 的延长线恰好经过点
的延长线恰好经过点![]() ,则
,则![]() 的长为( )
的长为( )
A. 1B. ![]() C. -1+
C. -1+![]() D.
D. ![]()
【答案】C
【解析】
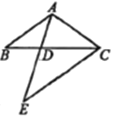
根据AB=AC可得∠B=∠ACB,由旋转性质可得DE=AB=2,∠ECD=∠ACB,∠E=∠B,进而可得∠E=∠ACD,因为∠EAC是公共角,可证明△DAC∽△CAE,所以![]() ,解方程可得AD的值,由于AD>0,即可得答案.
,解方程可得AD的值,由于AD>0,即可得答案.
∵AB=AC,
∴∠B=∠ACB,
∵将![]() 绕点
绕点![]() 逆时针方向旋转得到
逆时针方向旋转得到![]() ,
,
∴DE=AB=2,∠ECD=∠ACB,∠E=∠B,
∴∠E=∠ACD,
∵∠EAC=∠EAC,
∴△DAC∽△CAE,
∴![]() ,
,
∴22=AD(AD+2),
∴AD2+2AD-4=0,
解得:AD=![]() =
=![]() =-1
=-1![]() ,
,
∵AD>0,
∴AD=-1+![]() ,
,

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
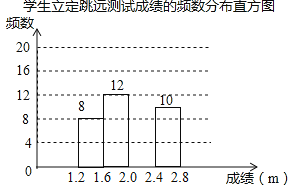
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?