题目内容
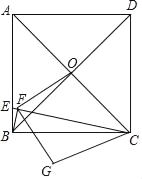
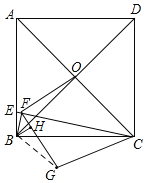
【题目】如图,正方形ABCD中,AD=4,E在AB上且AB=4BE,连接CE,作BF⊥CE于F,正方形对角线交于O点,连接OF,将△COF沿CE翻折得△CGF,连接BG,则BG的长为_____.
【答案】![]()
【解析】
Rt△BCE中,BF⊥CE,∠CBE=90°,可得BF=![]() =
=![]() ,再判定△COF∽△CEA,可得∠CFO=∠CAB=45°,进而得到∠CFG=∠CFO=45°,∠BFH=90°-45°=45°,可得△BFH是等腰直角三角形,再根据△COF∽△CEA,可得
,再判定△COF∽△CEA,可得∠CFO=∠CAB=45°,进而得到∠CFG=∠CFO=45°,∠BFH=90°-45°=45°,可得△BFH是等腰直角三角形,再根据△COF∽△CEA,可得![]() =
=![]() ,即
,即![]() =
=![]() ,进而得出OF=
,进而得出OF=![]() =GF,HG=FG-FH=
=GF,HG=FG-FH=![]() ,最后在Rt△BHG中,由勾股定理可得BG=
,最后在Rt△BHG中,由勾股定理可得BG=![]() =
=![]() .
.
解:如图,连接BG,过B作BH⊥GF于H,
由题可得,BE=1,BC=4,AE=3,OC=2![]() ,
,
∴Rt△BCE中,CE=![]() ,
,
∵BF⊥CE,∠CBE=90°,
∴BF=![]() =
=![]() ,
,
∵Rt△BCE中,BF⊥CE;Rt△ABC中,BO⊥AC,
∴BC2=CF×CE,BC2=CO×CA,
∴CF×CE=CO×CA,即![]() =
=![]() ,
,
又∵∠OCF=∠ECA,
∴△COF∽△CEA,
∴∠CFO=∠CAB=45°,
由折叠可得,∠CFG=∠CFO=45°,
∴∠BFH=90°-45°=45°,
∴△BFH是等腰直角三角形,
∴FH=BH=![]() BF=
BF=![]() ,
,
∵△COF∽△CEA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴OF=![]() =GF,
=GF,
∴HG=FG-FH=![]() ,
,
∴Rt△BHG中,BG=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目