题目内容
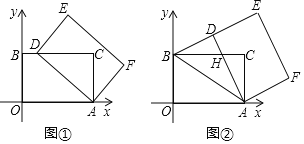
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,
(1)图①中共有 对相似三角形,写出来分别为 (不需证明);
(2)已知AB=10,AC=8,请你求出CD的长;
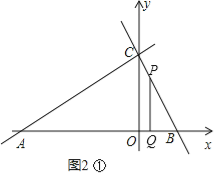
(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图②),若点P从点C出发,以每秒1个单位的速度沿线段CB运动,点Q从点B出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒,是否存在点P,使以点B,P,Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
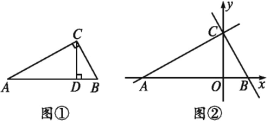
【答案】(1)3对,分别是:△ABC∽△ACD, △ABC∽△CBD , △ACD∽△CBD;(2)4.8;(3)存在,(1.35,3)或(3.15,1.8).
【解析】
试题(1)根据两角对应相等的两三角形相似即可得到3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)先在△ABC中由勾股定理求出BC的长,再根据△ABC的面积不变得到![]() ABCD=
ABCD=![]() ACBC,即可求出CD的长;
ACBC,即可求出CD的长;
(3)由于∠B公共,所以以点B、P、Q为顶点的三角形与△ABC相似时,分两种情况进行讨论:①△PQB∽△ACB;②△QPB∽△ACB.
试题解析:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD.
故答案为3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)如图1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,∴BC=![]() =6.
=6.
∵△ABC的面积=![]() ABCD=
ABCD=![]() ACBC,∴CD=
ACBC,∴CD=![]() =4.8;
=4.8;
(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:在△BOC中,∵∠COB=90°,BC=6,OC=4.8,∴OB=![]() =3.6.
=3.6.
分两种情况:①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,
∴![]() ,∴
,∴![]() ,解得t=2.25,即BQ=CP=2.25,
,解得t=2.25,即BQ=CP=2.25,
∴OQ=OB﹣BQ=3.6﹣2.25=1.35,BP=BC﹣CP=6﹣2.25=3.75.
在△BPQ中,由勾股定理,得PQ=![]() =
=![]() ,∴点P的坐标为(1.35,3);
,∴点P的坐标为(1.35,3);
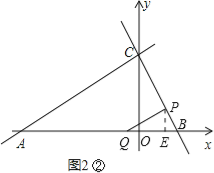
②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB,∴![]() ,∴
,∴![]() ,
,
解得t=3.75,即BQ=CP=3.75,BP=BC﹣CP=6﹣3.75=2.25.
过点P作PE⊥x轴于点E.
∵△QPB∽△ACB,∴![]() ,∴
,∴![]() ,∴PE=1.8.
,∴PE=1.8.
![]() =
=![]() ,∴OE=OB﹣BE=3.6﹣0.45=3.15,
,∴OE=OB﹣BE=3.6﹣0.45=3.15,
∴点P的坐标为(3.15,1.8);
综上可得,点P的坐标为(1.35,3)或(3.15,1.8).

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案