题目内容
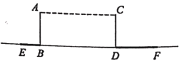
【题目】一天晚上,哥哥和弟弟拿两根等长的标杆![]() 直立在一盏亮着的路灯下,然后调整标杆位置,使它们在该路灯下的影子
直立在一盏亮着的路灯下,然后调整标杆位置,使它们在该路灯下的影子![]() 恰好在一条直线上(如图所示).
恰好在一条直线上(如图所示).
(1)请在图中画出路灯灯泡![]() 的位置;
的位置;
(2)哥哥和弟弟测得如下数据:![]() 米,
米,![]() 米,
米,![]() 米,两根标杆的距离
米,两根标杆的距离![]() 米,且
米,且![]() .请你根据以上信息计算灯泡
.请你根据以上信息计算灯泡![]() 距离地面的高度.
距离地面的高度.
【答案】(1)见解析;(2)3.52
【解析】
(1)连接FC、EA并延长,相交于点P,则点P即是灯泡的位置;(2)过P作PH⊥EF,则PH即是灯泡![]() 距离地面的高度,根据已知可得EF=6.6米,AB//PH//CD,即可证明
距离地面的高度,根据已知可得EF=6.6米,AB//PH//CD,即可证明![]() =
=![]() ,
,![]() =
=![]() ,由AB=CD可得
,由AB=CD可得![]() =
=![]() ,根据EH+FH=EF=6.6,解方程即可求出EH的长,进而根据
,根据EH+FH=EF=6.6,解方程即可求出EH的长,进而根据![]() =
=![]() 即可得答案.
即可得答案.
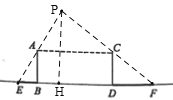
(1)如图所示,连接FC、EA并延长,相交于点P,则点P即是灯泡的位置;

(2)过P作PH⊥EF,则PH即是灯泡![]() 距离地面的高度,
距离地面的高度,
∵AC=BD=3.6米,BE=1米,DF=2米,
∴EF=BE+BD+DF=3.6+1+2=6.6(米),
∵AB⊥EF,CD⊥EF,PH⊥EF,且AB、CD、PH在同一平面内,
∴AB//CD//PH,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∵AB=CD,
∴![]() =
=![]()
∵FH=EF-EH,
∴![]() =
=![]() ,即
,即![]() ,
,
解得:EH=2.2(米),
∴![]() =
=![]() ,即
,即![]() =
=![]()
解得:PH=3.52(米).
答:灯泡![]() 距离地面的高度是3.52米.
距离地面的高度是3.52米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目