题目内容
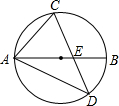
已知直角三角形ABC的三边长分别为a,b,c,∠C=90°,求它的内切圆的半径r.
小明同学求得的结果是r=
(a+b-c);小莉同学求得的结果是r=
.你认为他们解答的结果都正确吗?如果你认为他们的解答都是正确的,请帮助他们写出解答的过程.
小明同学求得的结果是r=
| 1 |
| 2 |
| ab |
| a+b+c |

都正确,.
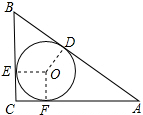
理由是:连接OA、OB、OC、OE、OF、OD,
∵⊙O切BC于E,切AB于D,切AC于F,
∴BE=BD,AD=AF,CE=CF,∠OEC=∠OFC=90°,
∵∠ACB=90°,OE=OF,
∴四边形CEOF是正方形,
∴OE=OF=CE=CF=r,
∴BE=BD=a-r,AD=AF=b-r,
∵AB=c,
∴b-r+a-r=c,
∴r=
(a+b-c);
∴小明求得的结果正确;
由三角形的面积公式得:S△ACB=S△BOC+S△AOC+S△AOB,
∴
ab=
ar+
br+
cr,
∴r=
,
∴小莉求得的结果正确.
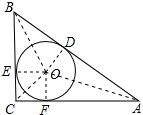
理由是:连接OA、OB、OC、OE、OF、OD,
∵⊙O切BC于E,切AB于D,切AC于F,
∴BE=BD,AD=AF,CE=CF,∠OEC=∠OFC=90°,
∵∠ACB=90°,OE=OF,
∴四边形CEOF是正方形,
∴OE=OF=CE=CF=r,
∴BE=BD=a-r,AD=AF=b-r,
∵AB=c,
∴b-r+a-r=c,
∴r=
| 1 |
| 2 |
∴小明求得的结果正确;
由三角形的面积公式得:S△ACB=S△BOC+S△AOC+S△AOB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| ab |
| a+b+c |
∴小莉求得的结果正确.


练习册系列答案
相关题目