题目内容
【题目】如图,D 是 AB 边上的中点,将△ABC 沿过点 D 的直线折叠,DE 为折痕,使点 A 落在 BC 上 F处,若∠B=40°,则∠EDF=_____度.

【答案】40
【解析】
先根据图形翻折不变的性质可得AD=DF,根据等边对等角的性质可得∠B=∠BFD,再根据三角形的内角和定理列式计算可得∠BDF的解,再根据平角的定义和折叠的性质即可求解.
∵△DEF是△DEA沿直线DE翻折变换而来,
∴AD=DF,
∵D是AB边的中点,
∴AD=BD,
∴BD=DF,
∴∠B=∠BFD,
∵∠B=50°,
∴∠BDF=180°-∠B-∠BFD=180°-40°-40°=100°,
∴∠EDF=(180°-∠BDF)÷2=40°.
故答案为40.

练习册系列答案
相关题目
【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
体育锻炼时间 | 人数 |
4≤x≤6 | |
2≤x<4 | 43 |
0≤x<2 | 15 |
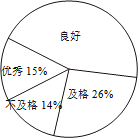
(1)试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;
(2)统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为x小时);
(3)全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.





