题目内容
【题目】如图， AD 为△ ABC 的中线， BE 为△ ABD 的中线．
（1）∠ ABE=15°，∠ BED=55°，求∠ BAD 的度数；
（2）作△ BED 的边 BD 边上的高；
（3）若△ ABC 的面积为 20， BD=2.5，求△ BDE 中 BD 边上的高.
【答案】(1)∠BAD =40°；（2）详见解析；（3）BD=2.5.
【解析】
（1）根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解；
（2）根据高线的定义，过点E作BD的垂线即可得解；
（3）根据三角形的中线把三角形分成的两个三角形面积相等，先求出△BDE的面积，再根据三角形的面积公式计算即可．
（1）在△ABE中，∵∠ABE=15°，∠BAD=40°，
∴∠BED=∠ABE+∠BAD=15°+40°=55°；
（2）如图，EF为BD边上的高；
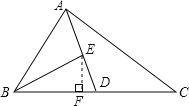
（3）∵AD为△ABC的中线，BE为△ABD的中线，
∴S△ABD=
S△ABC，S△BDE=S△ABD，S△BDE=
S△ABC，
∵△ABC的面积为20，BD=2.5，
∴S△BDE=BDEF=×5EF=×20，解得EF=2．
练习册系列答案
相关题目
【题目】九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
