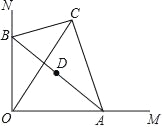
题目内容
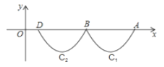
【题目】如图,抛物线 ![]() 与X轴交于点A、B,把抛物线在X轴及其下方的部分记作
与X轴交于点A、B,把抛物线在X轴及其下方的部分记作![]() ,将
,将![]() 向左平移得到
向左平移得到![]() ,
,![]() 与X轴交于点B、D,若直线
与X轴交于点B、D,若直线![]() 与
与![]() 、
、![]() 共有3个不同的交点,则m取值范围是( )
共有3个不同的交点,则m取值范围是( )
A. ![]() <m<
<m<![]() B.
B. ![]() <m<
<m<![]() C.
C. ![]() <m<
<m<![]() D.
D. ![]() <m<
<m<![]()
【答案】A
【解析】
首先求出点A和点B的坐标,然后求出C2解析式,分别求出直线y=![]() x+m与抛物线C2相切时m的值以及直线y=
x+m与抛物线C2相切时m的值以及直线y=![]() x+m过点B时m的值,结合图形即可得到答案.
x+m过点B时m的值,结合图形即可得到答案.
解:∵抛物线y=![]() 与x轴交于点A、B
与x轴交于点A、B
∴B(5,0),A(9,0)
∴抛物线向左平移4个单位长度
∴平移后解析式y=![]() (x-3)2-2
(x-3)2-2
当直线y=![]() x+m过B点,有2个交点
x+m过B点,有2个交点
∴0=![]() +m
+m
m=-![]()
当直线y=![]() x+m与抛物线C2相切时,有2个交点
x+m与抛物线C2相切时,有2个交点
∴![]() x+m=
x+m=![]() (x-3)2-2
(x-3)2-2
x2-7x+5-2m=0
∵相切
∴△=49-20+8m=0
∴m=-![]()
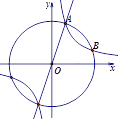
如图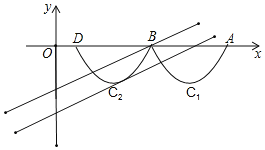
∵若直线y=![]() x+m与C1、C2共有3个不同的交点,
x+m与C1、C2共有3个不同的交点,
∴![]() <m<
<m<![]()
故选:A.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目