题目内容
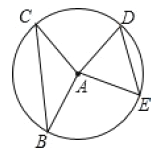
【题目】一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,
(1)求等边三角形的高;
(2)求CE的长度;
(3)若将等边三角形ABC绕点C顺时针旋转,旋转角为α(0°<α<360°),求α为多少时,等边三角形的边所在的直线与圆相切.

【答案】(1)2![]() ;(2)3;(3)α=60°或120°或180°或300°.
;(2)3;(3)α=60°或120°或180°或300°.
【解析】
(1)作AM⊥MC于M,在直角三角形ACM中,利用勾股定理即可解题,
(2)连接EF,在直角三角形CEF中, 利用勾股定理即可解题,
(3)画出图形即可解题.
解:(1)如图,作AM⊥MC于M.
∵△ABC是等边三角形,
∴∠MAC=∠MAB=30°,
∴CM=![]() AC=2,
AC=2,
∴AM=![]() =
=![]() =2
=2![]()
(2)∵CF是⊙O直径,
∴CF=CM=2![]() ,连接EF,则∠CEF=90°,
,连接EF,则∠CEF=90°,
∵∠ECF=90°﹣∠ACB=30°,
∴EF=![]() CF=
CF=![]() ,
,
∴CE=![]() =
=![]() =3.
=3.
(3)由图象可知,α=60°或120°或180°或300°时,等边三角形的边所在的直线与圆相切.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ | … | ﹣5 | ﹣3 | 2 | … |
植物高度增长量h/mm | … | 34 | 46 | 41 | … |
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃