题目内容
若正方形内切圆的面积πcm2,则它的外接圆的面积是( )cm2.
| A.2π | B.
| C.
| D.
|
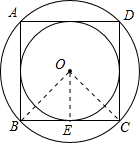
如图所示,连接OB、OC,过O作OE⊥BC;
∵四边形ABCD是正方形,
∴∠BOC=
=90°,
∵OB=OC,OE⊥BC,
∴∠BOE=
=
=45°,
∴BE=OE;
∵正方形ABCD的内切圆面积为πcm2,
∴OE=BE=1,
∴OB=
=
=
cm,
∴S外接圆=π(OB)2=π(
)2=2πcm2.
故选A.
∵四边形ABCD是正方形,
∴∠BOC=
| 4 |
| 360° |
∵OB=OC,OE⊥BC,
∴∠BOE=
| ∠BOC |
| 2 |
| 90° |
| 2 |
∴BE=OE;
∵正方形ABCD的内切圆面积为πcm2,
∴OE=BE=1,
∴OB=
| OE2+BE2 |
| 12+12 |
| 2 |
∴S外接圆=π(OB)2=π(
| 2 |
故选A.


练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目






