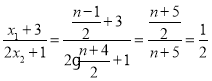题目内容
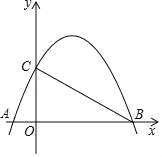
【题目】如图,已知直线y=﹣![]() x+2与x轴、y轴分别交于点B、C,抛物线y=﹣
x+2与x轴、y轴分别交于点B、C,抛物线y=﹣![]() +bx+c过点B、C,且与x轴交于另一个点A.
+bx+c过点B、C,且与x轴交于另一个点A.
(1)求该抛物线的表达式;
(2)点M是线段BC上一点,过点M作直线l∥y轴交该抛物线于点N,当四边形OMNC是平行四边形时,求它的面积;
(3)联结AC,设点D是该抛物线上的一点,且满足∠DBA=∠CAO,求点D的坐标.
【答案】(1)![]() ;(2)4;(3)(﹣5,﹣18)或(3,2).
;(2)4;(3)(﹣5,﹣18)或(3,2).
【解析】
(1)根据直线解析式求出点B、C的坐标,然后利用待定系数法求二次函数解析式列式求解即可;
(2)设M(m,-![]() m+2),则N(m,-
m+2),则N(m,-![]() m2+
m2+![]() m+2),则MN=(-
m+2),则MN=(-![]() m2+
m2+![]() m+2)-(-
m+2)-(-![]() m+2)=-
m+2)=-![]() m2+2m,根据MN=OC=2列方程可得M的横坐标,根据平行四边形的面积公式可得结论;
m2+2m,根据MN=OC=2列方程可得M的横坐标,根据平行四边形的面积公式可得结论;
(3)分两种情况:①当D在x轴的下方:根据AC∥BD,直线解析式k相等可设直线BD的解析式为:y=2x+b,把B(4,0)代入得直线BD的解析式为:y=2x-8,联立方程可得D的坐标;②当D在x轴的上方,根据对称可得M的坐标,利用待定系数法求直线BM的解析式,与二次函数的交点,联立方程可得D的坐标.
(1)当x=0时,y=2,
∴C(0,2),
当y=0时,﹣![]() x+2=0,x=4,
x+2=0,x=4,
∴B(4,0),
把C(0,2)和B(4,0)代入抛物线y=﹣![]() +bx+c中得:
+bx+c中得: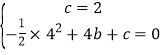 ,
,
解得:![]() ,
,
∴该抛物线的表达式:y=![]() ;
;
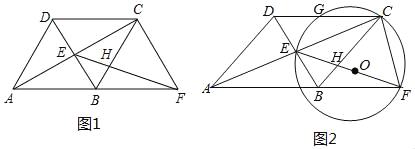
(2)如图1,
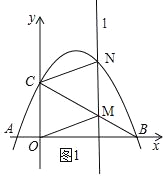
∵C(0,2),
∴OC=2,
设M(m,﹣![]() m+2),则N(m,
m+2),则N(m,![]() ),
),
∴MN=(![]() +2)﹣(﹣
+2)﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+2m,
m2+2m,
∵MN∥y轴,
当四边形OMNC是平行四边形时,MN=OC,
即﹣![]() m2+2m=2,
m2+2m=2,
解得:m1=m2=2,
∴Sspan>OCMN=OC×2=2×2=4;
(3)分两种情况:
当y=0时,﹣![]() +2=0,
+2=0,
解得:x1=4,x2=﹣1,
∴A(﹣1,0),
易得直线AC的解析式为:y=2x+2,
①当D在x轴的下方时,如图2,
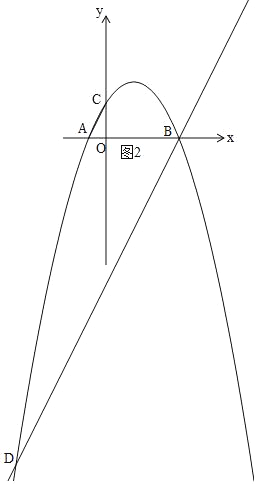
∵AC∥BD,
∴设直线BD的解析式为:y=2x+b,
把B(4,0)代入得:0=2×4+b,b=﹣8,
∴直线BD的解析式为:y=2x﹣8,
则2x﹣8=![]() +2,解得:x1=﹣5,x2=4(舍),
+2,解得:x1=﹣5,x2=4(舍),
∴D(﹣5,﹣18);
②当D在x轴的上方时,如图3,
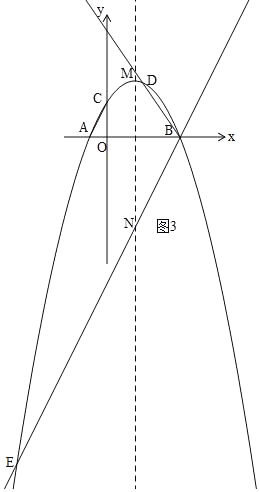
作抛物线的对称轴交直线BD于M,将BE(图2中的点D)于N,
对称轴是:x=﹣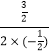 =
=![]() ,
,
∵∠CAO=∠ABE=∠DAB,
∴M与N关于x轴对称,
直线BE的解析式:y=2x﹣8,
当x=![]() 时,y=﹣5,
时,y=﹣5,
∴N(![]() ,﹣5),M(
,﹣5),M(![]() ,5),
,5),
直线BM的解析式为:y=﹣2x+8,
﹣2x+8=﹣![]() +2,解得:x1=3,x2=4(舍),
+2,解得:x1=3,x2=4(舍),
∴D(3,2),
综上所述,点D的坐标为:(﹣5,﹣18)或(3,2).