题目内容
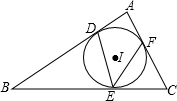 如图,⊙I是△ABC的内切圆,D,E,F为三个切点,若∠DEF=52°,则∠A的度数为
如图,⊙I是△ABC的内切圆,D,E,F为三个切点,若∠DEF=52°,则∠A的度数为
- A.76°
- B.68°
- C.52°
- D.38°
A
分析:连接ID、IF,在⊙I中,由圆周角定理可求得∠DIF的度数,在四边形EDFA中,由于∠IDA=∠IFA=90°,因此∠DIF和∠A互补,由此求出∠A的度数.
解答: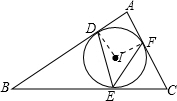 解:连接ID、IF;
解:连接ID、IF;
∵⊙I是△ABC的内切圆,
∴ID⊥AB,IF⊥AC;
又∵⊙I中,∠DIF=2∠DEF=104°,
四边形DIFA中,∠IDA=∠IFA=90°,
∴∠A=180°-∠DIF=76°,
故选A.
点评:此题主要考查了三角形内切圆的性质以及圆周角定理、多边形的内角和等知识,难度不大.
分析:连接ID、IF,在⊙I中,由圆周角定理可求得∠DIF的度数,在四边形EDFA中,由于∠IDA=∠IFA=90°,因此∠DIF和∠A互补,由此求出∠A的度数.
解答:
 解:连接ID、IF;
解:连接ID、IF;∵⊙I是△ABC的内切圆,
∴ID⊥AB,IF⊥AC;
又∵⊙I中,∠DIF=2∠DEF=104°,
四边形DIFA中,∠IDA=∠IFA=90°,
∴∠A=180°-∠DIF=76°,
故选A.
点评:此题主要考查了三角形内切圆的性质以及圆周角定理、多边形的内角和等知识,难度不大.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
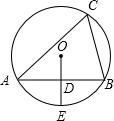 如图,⊙O是△ABC的外接圆,OD⊥AB于点D、交⊙O于点E,∠C=60°,如果⊙O的半径为2,那么OD=
如图,⊙O是△ABC的外接圆,OD⊥AB于点D、交⊙O于点E,∠C=60°,如果⊙O的半径为2,那么OD=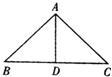 24、如图,AD是△ABC的高,且AD平分∠BAC,请指出∠B与∠C的关系,并说明理由.
24、如图,AD是△ABC的高,且AD平分∠BAC,请指出∠B与∠C的关系,并说明理由.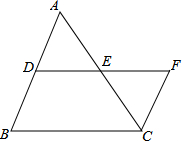 (2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( )
(2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( ) (2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
(2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.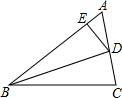 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.