题目内容
【题目】先阅读材料,再解答问题:
已知点![]() 和直线
和直线![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.例如:求点
计算.例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线![]() 可知:
可知:![]() .
.
所以点![]() 到直线
到直线![]() 的距离为
的距离为![]()
![]() .
.
求:(1)已知直线![]() 与
与![]() 平行,求这两条平行线之间的距离;
平行,求这两条平行线之间的距离;
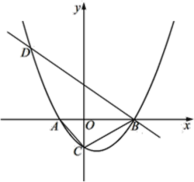
(2)已知直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点,
两点,![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,![]() 为
为![]() 上的动点,试求
上的动点,试求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)18
;(2)18
【解析】
(1)在直线![]() 上任取一点
上任取一点![]() ,由直线
,由直线![]() 与
与![]() 平行,则两直线间的距离即为点P到
平行,则两直线间的距离即为点P到![]() 的距离;再根据题干所给距离公式解答即可;
的距离;再根据题干所给距离公式解答即可;
(2)分别令x=0、y=0求得对应的y和x,进而确定点A、B的坐标和AB的长度;设圆心![]() 到直线
到直线![]() 即
即![]() 的距离为
的距离为![]() ,
,![]() 的半经为
的半经为![]() ,然后根据题干所给距离公式求得半径R,然后再根据直线与圆的位置关系列出不等式,求得点
,然后根据题干所给距离公式求得半径R,然后再根据直线与圆的位置关系列出不等式,求得点![]() 到直线
到直线![]() 的距离的最大值,最后运用圆的面积公式求解即可.
的距离的最大值,最后运用圆的面积公式求解即可.
解:(1)在直线![]() 上任取一点
上任取一点![]() ,
,
![]() 直线
直线![]() 与
与![]() 平行,
平行,
![]() 这两条平行线之间的距离等于点
这两条平行线之间的距离等于点![]() 到直线
到直线![]() 的距离.
的距离.
![]() 直线
直线![]() 可变形为
可变形为![]() ,其中
,其中![]() .
.
![]() 点
点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
![]() 这两条平行线之间的距离等于
这两条平行线之间的距离等于![]() ;
;
(2)令![]() 得
得![]() ;令
;令![]() 得
得![]()
![]()
![]() ,
,![]() .
.![]()
设圆心![]() 到直线
到直线![]() 即
即![]() 的距离为
的距离为![]() ,
,![]() 的半经为
的半经为![]()
![]()
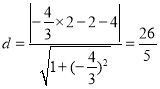 ,即:
,即:![]()
又∵![]() 上任意点
上任意点![]() 到直线
到直线![]() 的距离h≤
的距离h≤![]() ,
,
![]()
![]() 上任意点
上任意点![]() 到直线
到直线![]() 的距离的最大值hmax=
的距离的最大值hmax=![]()
所以![]() 的面积的最大值为:
的面积的最大值为:
![]() .
.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目