Question

【题目】如图，信号塔PQ座落在坡度i=1：2的山坡上，其正前方直立着一警示牌．当太阳光线与水平线成60°角时，测得信号塔PQ落在斜坡上的影子QN长为2 米，落在警示牌上的影子MN长为3米，求信号塔PQ的高．（结果不取近似值）

Answer 1

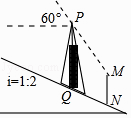
【答案】解：如图作MF⊥PQ于F，QE⊥MN于E，则四边形EMFQ是矩形．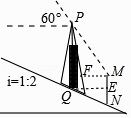

在Rt△QEN中，设EN=x，则EQ=2x，
∵QN2=EN2+QE2 ，
∴20=5x2 ，
∵x＞0，
∴x=2，
∴EN=2，EQ=MF=4，
∵MN=3，
∴FQ=EM=1，
在Rt△PFM中，PF=FMtan60°=4 ，
∴PQ=PF+FQ=4 +1
【解析】如图作MF⊥PQ于F，QE⊥MN于E，则四边形EMFQ是矩形．分别在Rt△EQN、Rt△PFM中解直角三角形即可解决问题．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对关于坡度坡角问题的理解，了解坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA．