��Ŀ����
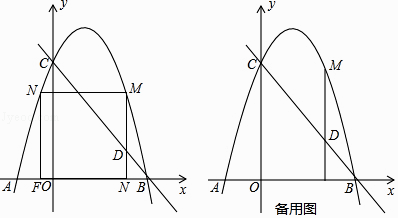
����Ŀ����֪��ƽ��ֱ������ϵxOy�У���ͼ������֪������y=��x2+bx+c������A��2��2�����Գ�����ֱ��x=1������ΪB��
��1�������������ߵı���ʽ�͵�B�����ꣻ
��2����M�ڶԳ����ϣ���λ�ڶ����Ϸ���������������Ϊm������AM���ú�m�Ĵ���ʽ��ʾ��AMB������ֵ��
��3���������������ϻ�����ƽ�ƣ�ʹ���������ߵĶ���C��x���ϣ�ԭ��������һ��Pƽ�ƺ�Ķ�Ӧ��Ϊ��Q�����OP=OQ�����Q�����꣮
���𰸡�
��1��
�⣺�������ߵĶԳ���Ϊx=1��
��x=�� ![]() =1����
=1���� ![]() =1�����b=2��
=1�����b=2��
��y=��x2+2x+c��
��A��2��2������ã���4+4+c=2����ã�c=2��
�������ߵĽ���ʽΪy=��x2+2x+2��
�䷽�ã�y=����x��1��2+3��
�������ߵĶ�������Ϊ��1��3��
��2��
�⣺��ͼ��ʾ������A��AC��BM������ΪC����AC=1��C��1��2����

��M��1��m����C��1��2����
��MC=m��2��
��cot��AMB= ![]() =m��2
=m��2
��3��
�⣺�������ߵĶ�������Ϊ��1��3����ƽ�ƺ������ߵĶ���������x���ϣ�
������������ƽ����3����λ��
��ƽ�ƺ������ߵĽ���ʽΪy=��x2+2x��1��PQ=3��
��OP=OQ��
���O��PQ�Ĵ�ֱƽ�����ϣ�
�֡�QP��y�ᣬ
���Q���P����x��Գƣ�
���Q���������� ![]() ��
��
��y=�� ![]() ����y=��x2+2x��1���x2+2x��1=��
����y=��x2+2x��1�ã���x2+2x��1=�� ![]() ����ã�x=
����ã�x= ![]() ��x=
��x= ![]() ��
��
���Q�������� ![]() ����
���� ![]() ����
���� ![]() ����
���� ![]() ��
��
����������1�����������ߵĶԳ��᷽�̿����b��ֵ��Ȼ��A���������y=��x2+2x+c�����c��ֵ����2������A��AC��BM������ΪC���Ӷ��ɵõ�AC=1��MC=m��2���������������Ǻ����Ķ�����⼴�ɣ���3����ƽ�ƺ������ߵĶ�����x���Ͽ����ƽ�Ƶķ���;��룬�ʴ�QP=3��Ȼ���ɵ�QO=PO��QP��y��ɵõ���Q��P����x�Գƣ�����õ�Q�������꣬����Q�����������ƽ�ƺ�Ľ���ʽ����ö�Ӧ��x��ֵ����ɵõ���Q�����꣮
�����㾫����������Ĺؼ�����������κ���ͼ���ƽ�Ƶ����֪ʶ������ƽ�Ʋ��裺��1���䷽ y=a(x-h)2+k��ȷ�����㣨h,k����2����x������Ҽ�����y���ϼ��¼����Լ���������Ǻ����Ķ�������⣬�˽����A�����ҡ����ҡ����С����ж�������A��������Ǻ�����

����Ŀ��ijУ��������ѡ�ν�Ŀ�����У��ӱ�ѡ�ġ����衱������ʿ���������塱�������������������赸�У�ѡ��һ��ѧ����ϲ�����赸��Ϊ�ˣ���������˱�У�IJ���ѧ�����������������Ƴ�����ͳ��ͼ����ÿλѧ��ֻѡ��һ�����ͣ�������ͳ��ͼ������Ϣ������������⣺
���� | ���� | ���� | ��ʿ | ���� |
�ݵ�ٷֱ� | a | 30% | b | 15% |

��1�����γ��������ѧ��������a��b��ֵ��
��2��������ͳ��ͼ����������
��3������У����1500��ѧ�����Թ���ȫУϲ���������赸����ѧ��������