题目内容
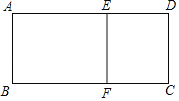
【题目】如图所示,用一根长度为18米的原材料制作一个矩形窗户边框(即矩形ABFE和矩形DCFE),原材料刚好全部用完,设窗户边框AB长度为x米,窗户总面积为S平方米(注:窗户边框粗细忽略不计).
(1)求S与x之间的函数关系式;
(2)若窗户边框AB的长度不少于2米,且边框AB的长度小于BC的长度,求此时窗户总面积S的最大值和最小值.
【答案】(1)S=﹣![]() x2+9x;(2)窗户总面积S的最大值是
x2+9x;(2)窗户总面积S的最大值是![]() m2、最小值是12m2.
m2、最小值是12m2.
【解析】
(1)根据题意和图形可以求得S与x的函数表达式;
(2)根据题意可以得到关于x的不等式,然后根据(1)中的函数解析式和二次函数的性质可以解答本题.
(1)由题意可得,
S=x![]() =﹣
=﹣![]() x2+9x,
x2+9x,
即S与x的函数表达式是S=﹣![]() x2+9x;
x2+9x;
(2)由题意可得,
2≤x<![]() ,
,
解得,2≤x<3.6,
∵S=﹣![]() x2+9x,2≤x<3.6,
x2+9x,2≤x<3.6,
∴当x=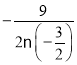 =3时,S取得最大值,此时S=
=3时,S取得最大值,此时S=![]() ,
,
当x=2时,S取得最小值,此时S=12,
答:窗户总面积S的最大值是![]() m2、最小值是12m2.
m2、最小值是12m2.

【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值