题目内容
已知在平面直角坐标系中，点A（3，2），B（2，-1），点P在x轴上运动，为使|PA-PB|最大，则点P的坐标为______．
作出B关于x轴的对称点B′，连接AB′，与x轴交于C点，D为x轴上除去D的任意一点，连接AD，BD，B′D，
可得B′（2，1），
设直线AB′的解析式为y=kx+b（k≠0），
将A和B′的坐标代入得：
，
解得：
，
故直线AB解析式为y=x-1，
令y=0，解得x=1，即D坐标为（1，0），
则P位于D点位置时，|PA-PB|最大，此时P坐标为（1，0）．
故答案为：（1，0）．
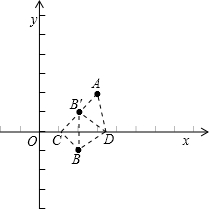
可得B′（2，1），
设直线AB′的解析式为y=kx+b（k≠0），
将A和B′的坐标代入得：
|
解得：
|
故直线AB解析式为y=x-1，
令y=0，解得x=1，即D坐标为（1，0），
则P位于D点位置时，|PA-PB|最大，此时P坐标为（1，0）．
故答案为：（1，0）．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
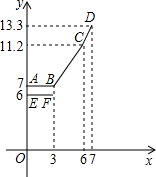表示y2与x之间的函数关系式，线段EF表示当0≤x≤3时，y1与x的函数关系式，根据图表信息，完成下列各题：
）与生产时间t（小时）的函数关系如图所示．