题目内容
【题目】将纸片△ABC沿AD折叠,使点C刚好落在AB边上的E处,展开如图1.
[操作观察]
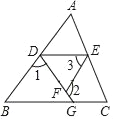
(1)如图2,作DF⊥AC,垂足为F,且DF=3,AC=6,S△ABC=21,则AB= ;
[理解应用]
(2)①如图3,设G为AC上一点(与A、C)不重合,P是AD上一个动点,连接PG、PC.试说明:PG+PC与EG大小关系;
②连接EC,若∠BAC=60°,G为AC中点,且AC=6,求EC长.
[拓展延伸]
(3)请根据前面的解题经验,解决下面问题:
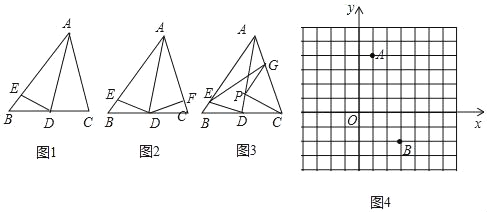
如图4,在平面直角坐标系中有A(1,4),B(3,﹣2),点P是x轴上的动点,连接AP、BP,当AP﹣BP的值最大时,请在图中标出P点的位置,并直接写出此时P点的坐标为 ,AP﹣BP的最大值为 .
【答案】(1)8;(2)①PG+PC≥EG,理由见解析;②连6;(3)(5,0),2![]() .
.
【解析】
(1)根据折叠的特性可知折痕AD为∠BAC的角平分线,由此可得出点D到AB和点D到AC的距离相等,再根据三角形的面积公式即可得出结论;
(2)连接CM、PE、CE,根据三角形两边之和大于第三边得出当点P与点M重合时,PF+PC值最小,再根据折叠的性质得出AE=AC,结合∠BAC=60°即可得出△AEC为等边三角形,由此即可解决问题;
(3)作点B关于x轴的对称点B′,连接AB′、PB′,延长AB′交x轴于点P′,根据三角形内两边之差小于第三边找出当点P和P′点重合时,AP﹣BP的值最大,再由点B的坐标可得出点B′的坐标,结合点A、B′的坐标即可求出直线AB′的解析式,令其y=0求出x即可找出点P′的坐标,由此即可得出结论.
(1)∵将纸片△ABC沿AD折叠,使C点刚好落在AB边上的E处,∴AD为∠BAC的角平分线,∴点D到AB和点D到AC的距离相等,∴S△ABC=![]() ABDF+
ABDF+![]() ACDF=21,∴
ACDF=21,∴![]() AB3+
AB3+![]() ×6×3=21,∴AB=8.
×6×3=21,∴AB=8.
故答案为:8.
(2)①结论:PG+PC≥EG.理由如下:
连接PE,如图3所示.

∵将纸片△ABC沿AD折叠,使C点刚好落在AB边上的E处,∴AD为∠BAC的角平分线,AE=AC,∴PE=PC.在△PEG中,PE+PG≥EG,∴PC+PG≥EG.
②连接EC,如图3中.
∵AE=AC,∠BAC=60°,∴△AEC为等边三角形.
又∵AC=6,∴EC=AC=6.
(3)作点B关于x轴的对称点B′,连接AB′、PB′,延长AB′交x轴于点P′,如图4所示.

∵点B和B′关于x轴对称,∴PB=PB′,P′B′=P′B.
∵在△APB′中,AB′>AP﹣PB′,∴AP′﹣B′P′=AP′﹣BP′=AB′>AP﹣PB′=AP﹣PB,∴当点P与点P′重合时,AP﹣BP最大.
设直线AB′的解析式为y=kx+b.
∵点B(3,﹣2),∴点B′(3,2),AB′=![]() =
=![]() =2
=2![]() .
.
将点A(1,4)、B′(3,2)代入y=kx+b中,得:![]() ,解得:
,解得:![]() ,∴直线AB′的解析式为y=﹣x+5.
,∴直线AB′的解析式为y=﹣x+5.
令y=﹣x+5中y=0,则﹣x+5=0,解得:x=5,∴点P′(5,0).
故AP﹣BP的最大值为2![]() ,此时P点的坐标为(5,0).
,此时P点的坐标为(5,0).
故答案为:(5,0),2![]() .
.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案