题目内容
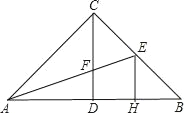
【题目】如图,在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,EH⊥AB于点H,那么CF=EH吗?说明理由.
【答案】详见解析.
【解析】
根据角平分线的性质得出CE=HE,∠CAE=∠EAH,再由两角互补的性质得出∠AEC=∠AEH,根据平行线的性质得出∠EFC=∠AEH,所以∠AEC=∠EFC,即可证得结论.
∵在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,EH⊥AB于点H,
∴CE=HE,∠CAE=∠EAH,
∵∠CAE+∠AEC=90°,∠EAH+∠AEF=90°
∴∠AEC=∠AEH,
∵CD⊥AB,EH⊥AB,
∴CD∥EH,
∴∠EFC=∠AEH,
∴∠AEC=∠EFC,
∴CE=CF,
∴CF=EH.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目