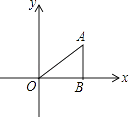��Ŀ����
����Ŀ�����Ķ�����ͼ1���ı���OABC�У�OA=a��OC=3��BC=2��
��AOC=��BCO=90����������O��ֱ��l���ı��ηֳ������֣�ֱ��l��OC���ɵĽ���Ϊ�������ı���OABC��ֱ����OCB��ֱ��l�۵�����C���ڵ�D�������ǰ�����������̼�ΪFZ[�ȣ�a]��
�����⣩
����D���A�غϣ��������������ΪFZ[45�㣬3]��
�����ԣ�
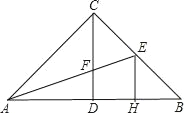
��1������DǡΪAB���е㣨��ͼ2�������ȣ�
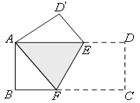
��2������FZ[45�㣬a]��������B���ڵ�E��������E���ı���OABC�ı�AB�ϣ����a��ֵ������E�����ı���OABC���ⲿ��ֱ��д��a��ȡֵ��Χ��

���𰸡���1���� =30�㣻��2����0��a��5ʱ����E�����ı���0ABC���ⲿ��
��������
��1���ȸ���ASA�����ó���BCD�ա�AFD���ʿɵó�CD=FD������DΪRt��COFб��CF���е㣬���۵���֪��OD=OC����OD=OC=CD����OCDΪ�ȱ������Σ���COD=60�㣬���ݵȱ����������ߺ�һ�����ʿɵó����ۣ���2�����ݵ�E�ı���0ABC�ı�AB�Ͽ�֪AB��ֱ��l���������۵���֪��OD=OC=3��DE=BC=2�����ɦ�=45�㣬AB��ֱ��l���ó���ADEΪ����ֱ�������Σ��ʿɵó�OA�ij����ɴ˿ɵó����ۣ�
��1������CD���ӳ�����OA�ӳ����ڵ�F��
����BCD����AFD��
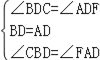 ��
��
���BCD�ա�AFD��ASA����
��CD=FD������DΪRt��COFб��CF���е㣬
��OD=![]() CF=CD��
CF=CD��
�����۵���֪��OD=OC��
��OD=OC=CD��
���OCDΪ�ȱ������Σ���COD=60�㣬
���=![]() ��COD=30�㣻
��COD=30�㣻
��2������E�ı���OABC�ı�AB�ϣ�
��AB��ֱ��l
���۵���֪��OD=OC=3��DE=BC=2��
�ߦ�=45�㣬AB��ֱ��l��
���ADEΪ����ֱ�������Σ�
��AD=DE=2��
��OA=OD+AD=3+2=5��
��a=5��
��ͼ��֪����0��a��5ʱ����E�����ı���0ABC���ⲿ��