题目内容
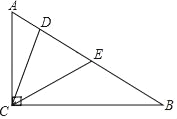
【题目】如图,在△ACB中,∠ACB=90°,D、E为斜边AB上的两点,且BD=BC,AE=AC,求∠DCE的度数.
【答案】45°
【解析】
已知BD=BC,AE=AC,根据等腰三角形的性质可得∠BCD=∠BDC,∠AEC=∠ACE,即可得∠BCE+∠DCE=∠BDC,∠ACD+∠DCE=∠AEC,又因∠DCE+∠BDC+∠AEC=180°,所以∠BCE+∠DCE+∠ACD+∠DCE+∠DCE=180°,再由∠ACB=90°,可得∠BCE+∠DCE+∠ACD=90°,所以2∠DCE=180°﹣90°,即可求得∠DCE=45°.
∵BD=BC,AE=AC,
∴∠BCD=∠BDC,∠AEC=∠ACE,
即∠BCE+∠DCE=∠BDC,∠ACD+∠DCE=∠AEC,
∵∠DCE+∠BDC+∠AEC=180°,
∴∠BCE+∠DCE+∠ACD+∠DCE+∠DCE=180°,
又∠ACB=90°,
∴∠BCE+∠DCE+∠ACD=90°,
∴2∠DCE=180°﹣90°,
∴∠DCE=45°.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目