题目内容
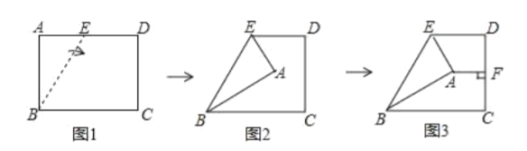
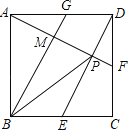
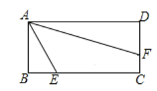
【题目】如图,在矩形ABCD中,AB=3,BC=6,点E,F分别在BC,CD上,若BE=![]() ,∠EAF=45°,则AF=_____.
,∠EAF=45°,则AF=_____.
【答案】![]()
【解析】
如图,作正方形ABNM,MN与AF交于点G,连接EG,延长EB至H,使BH=MG,连接AH,证△AMG≌△ABH,△GAE≌△HAE,根据全等三角形的性质得出EG=HE=BE+MG,设MG=x,根据全等三角形的性质得到用x表示出MG,根据勾股定理求出MG,根据相似三角形的性质求出DF,利用勾股定理即可求出AF的长.
如图,作正方形ABNM,MN与AF交于点G,连接EG,延长EB至H,使BH=MG,连接AH,

∵在正方形ABNM中,
∴∠AMG=∠ABH,AM=AB,
在△AMG和△ABH中,
∵ ,
,
∴△AMG≌△ABH(SAS),
∴∠BAH=∠GAM,AG=AH,
∴∠GAH=90°,
∴∠EAG=∠EAH=45°,
在△GAE和△HAE中,
∵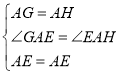 ,
,
∴△GAE≌△HAE(SAS),
∴EG=HE=BE+HB,
∴EG=BE+MG,
设MG=x,则NG=3-x,EG=x+![]() ,
,
在Rt△GEN中,EG2=NG2+NE2,即(x+![]() )2=(3﹣x)2+
)2=(3﹣x)2+![]() ,
,
解得:x=1,即MG=1,
∵MN∥CD,
∴△AGM∽△AFD,
∴![]() ,即
,即![]() ,
,
解得:DF=2,
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】小明的爸爸想给妈妈送张美容卡作为生日礼物,小明家附近有 3 家美容店,爸爸不知 如何选择,于是让小明对 3 家店铺顾客的满意度做了调查:
|
|
| 合计 | |
美容店 A | 53 | 28 | 19 | 100 |
美容店 B | 50 | 40 | 10 | 100 |
美容店 C | 65 | 26 | 9 | 100 |
(说明:顾客对于店铺的满意度从高到低,依次为 3 个笑脸,2 个笑脸,1 个笑脸) 小明选择将_____(填“A”、“ B”或“C”)美容店推荐给爸爸,能使妈妈获得满意体验可能性最大.