题目内容
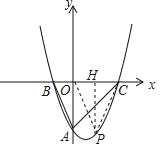
【题目】如图在直角坐标平面内,抛物线y=ax2+bx﹣3与y轴交于点A,与x轴分别交于点B(﹣1,0)、点C(3,0),点D是抛物线的顶点.

(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、DC,求△ACD的面积;
(3)点P在直线DC上,联结OP,若以O、P、C为顶点的三角形与△ABC相似,求点P的坐
标.
【答案】(1)y=(x﹣1)2﹣4,D的坐标是(1,﹣4);(2)3;(3)P1(![]() ,﹣
,﹣![]() )或P2(2,﹣2).
)或P2(2,﹣2).
【解析】
(1)将B、C的坐标代入抛物线y=ax2+bx﹣3,即可求出表达式,将表达式写成顶点式,即可直接写出D点坐标.
(2)先求出△ACD三边的长度,利用勾股定理逆定理判定△ACD是直角三角形,从而求出面积.
(3)先说明∠BAC=∠BCD,∠BCD即为△OPC中的∠OCP,接下来分情况讨论另外有一对角相等时△OPC与△ABC.
解:(1)点B(﹣1,0)、C(3,0)在抛物线y=ax2+bx﹣3上,
∴![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为:y=x2﹣2x﹣3=(x﹣1)2﹣4,
故顶点D的坐标是(1,﹣4);
(2)∵A(0,﹣3),C(3,0),D(1,﹣4),
∴AC=3![]() ,CD=2
,CD=2![]() ,AD=
,AD=![]() ,
,
∴CD2=AC2+AD2,
∴∠CAD=90°,
∴S△ACD=![]() ACAD=
ACAD=![]() ×3
×3![]() ×
×![]() =3;
=3;
(3)∵∠CAD=∠AOB=90°,![]() =
=![]() =
=![]() ,
,
∴△CAD∽△AOB,
∴∠ACD=∠OAB,
∵OA=OC,∠AOC=90°,
∴∠OAC=∠OCA=45°,
∴∠OAC+∠OAB=∠OCA+∠ACD,即∠BAC=∠BCD,
若以O、P、C为顶点的三角形与△ABC相似,且△ABC为锐角三角形,
则△POC也为锐角三角形,点P在第四象限,
由点C(3,0),D(1,﹣4)得直线CD的表达式是:y=2x﹣6,设P(t,2t﹣6)(0<t<3)
过P作PH⊥OC,垂足为点H,则OH=t,PH=6﹣2t,
①当∠POC=∠ABC时,由tan∠POC=tan∠ABC得![]() =
=![]() ,
,
∴![]() =3,
=3,
解得:t=![]() ,
,
∴P1(![]() ,﹣
,﹣![]() );
);
②当∠POC=∠ACB时,由tan∠POC=tan∠ACB=tan45°=1,得![]() =1,
=1,
∴![]() =1,
=1,
解得:t=2,
∴P2(2,﹣2),
综上得:P1(![]() ,﹣
,﹣![]() )或P2(2,﹣2).
)或P2(2,﹣2).
故答案为:(1)y=(x﹣1)2﹣4,D的坐标是(1,﹣4);(2)3;(3)P1(![]() ,﹣
,﹣![]() )或P2(2,﹣2).
)或P2(2,﹣2).