题目内容
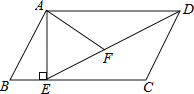
【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为__.

【答案】![]() 或
或![]() .
.
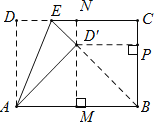
【解析】如图,连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P,已知点D的对应点D′落在∠ABC的角平分线上,可得MD′=PD′,设MD′=x,则PD′=BM=x,即可得AM=AB-BM=7-x,由折叠图形的性质可得AD=AD′=5,即x2+(7-x)2=25,解得x=3或4,即MD′=3或4.在Rt△END′中,设ED′=a,①当MD′=3时,AM=7-3=4,D′N=5-3=2,EN=4-a,由勾股定理可得a2=22+(4-a)2,解得a=![]() ,即DE=
,即DE=![]() ,②当MD′=4时,AM=7-4=3,D′N=5-4=1,EN=3-a,由勾股定理可得a2=12+(3-a)2,解得a=
,②当MD′=4时,AM=7-4=3,D′N=5-4=1,EN=3-a,由勾股定理可得a2=12+(3-a)2,解得a=![]() ,即DE=
,即DE=![]() ,所以DE的长为
,所以DE的长为![]() 或
或![]() .
.

练习册系列答案
相关题目