Question

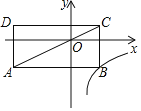
【题目】如图，在直角坐标系中，矩形ABCD的对角线AC经过坐标原点O，矩形的边分别平行于坐标轴，点B在函数y=（k≠0，x>0）的图像上，点D的坐标为（-4,1），则K的值为（ ）

A.B.C.4D.-4

Answer 1

【答案】D

【解析】

由于点B的坐标不能求出，但根据反比例函数的几何意义只要求出矩形OEBF的面积也可，依据矩形的性质发现S矩形OGDH=S矩形OEBF，而S矩形OGDH可通过点D（-4，1）转化为线段长而求得．，在根据反比例函数的所在的象限，确定k的值即可．

如图，根据矩形的性质可得：S矩形OGDH=S矩形OEBF，

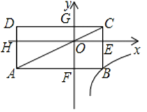
∵D（-4，1），

∴OH=4，OG=1，

∴S矩形OGDH=OHOG=4，

设B（a，b），则OE=a，OF=-b，

∴S矩形OEBF=OEOF=-ab=4，

又∵B（a，b）在函数y＝（k≠0，x＞0）的图象上，

∴k=ab=-4

故选：D．