Question

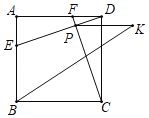
【题目】如图，正方形ABCD中，AB＝4，E，F分别是边AB，AD上的动点，AE＝DF，连接DE，CF交于点P，过点P作PK∥BC，且PK＝2，若∠CBK的度数最大时，则BK长为_____．

Answer 1

【答案】6．

【解析】

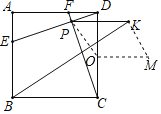
根据全等三角形的性质得到∠ADE＝∠DCF，求得∠CPD＝90°，得到点P在以CD为直径的半圆上运动，取CD的中点O，过O作OM⊥CD，且点M在CD的右侧，MO＝2，连接OP，KM，推出四边形POMK是菱形，于是得到点K在以M为圆心，半径＝2的半圆上运动，当BK与⊙M相切时，∠CBK最大，根据勾股定理即可得到结论．

解：∵正方形ABCD中，AD＝CD，∠A＝∠CDA＝90°，

∵AE＝DF，

∴△ADE≌△DCF（SAS），

∴∠ADE＝∠DCF，

∵∠ADE+∠CDE＝90°，

∴∠DCF+∠CDE＝90°，

∴∠CPD＝90°，

∴点P在以CD为直径的半圆上运动，

取CD的中点O，过O作OM⊥CD，且点M在CD的右侧，MO＝2，

连接OP，KM，

∵PK∥BC，BC⊥CD，

∴PK⊥CD，

∴PK∥OM，PK＝OM＝2，

∴四边形POMK是平行四边形，

∵CD＝AB＝4，

∴OP＝CD＝2，

∴OP＝OM，

∴四边形POMK是菱形，

∴点K在以M为圆心，半径＝2的半圆上运动，

当BK与⊙M相切时，∠CBK最大，

∴∠BKM＝90°，

∵BM＝＝2，

∴BK＝＝6，

故答案为：6．