��Ŀ����
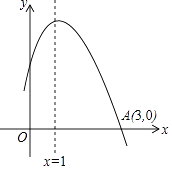
����Ŀ����֪��������y=ax+bx+4��x�ύ�ڵ�A��-3��0����B��2��0������y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
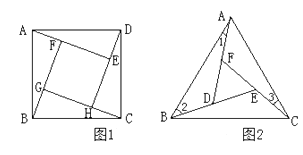
��2����ͼ1������DΪCB���е㣬���߶�DB�Ƶ�D��ת����B�Ķ�Ӧ��Ϊ��G������Gǡ�����������ߵĶԳ�����ʱ�����G�����ꣻ
��3����ͼ2������DΪֱ��BC��ֱ��AC�ϵ�һ�㣬EΪx����һ���㣬������![]() �Գ������Ƿ���ڵ�F��ʹ��B��D��F��EΪ������ı���Ϊ���Σ������ڣ��������F�����ꣻ�������ڣ���˵�����ɣ�
�Գ������Ƿ���ڵ�F��ʹ��B��D��F��EΪ������ı���Ϊ���Σ������ڣ��������F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
��A��-3��0����B��2��0�����ã� ![]()
�� ![]() = ax+bx+4
= ax+bx+4
�� ![]()
�� ![]()
�� ![]() .
.
��2��
��C��0,4������BC= ![]() .
.
�� ![]() �ɶԳ���Ϊx=
�ɶԳ���Ϊx= 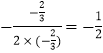 ,
,
������G������Ϊ ![]() ��
��
�ߵ�D��BC���е�
���D������Ϊ ![]() ��
�� ![]()
����ת�ɵã�DG=DB
�� ![]() ����������
����������
�� ![]() ������
������
���G������Ϊ ![]() ��
�� ![]()
��3��
�ٵ�BEΪ�Խ���ʱ����Ϊ���εĶԽ����ഹֱƽ�֣����Դ�ʱD��Ϊ�Գ�����AC�Ľ����Գ����BC�Ľ��㣬FΪ��D����x��ĶԳƵ㣬
�� ![]() ��
��
��C ![]() ��A
��A ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�൱ ![]() ʱ��
ʱ�� ![]() ��
��
��D ![]() ��
��
��F ![]() ��
��
�� ![]()
�൱ ![]() ʱ��y=5��
ʱ��y=5��
��D ![]() ��
��
��F ![]() ��
��
�ڵ�BEΪ���εı�ʱ����DF��BE
I)����D��ֱ��BC��ʱ
![]()
��D ![]() �����F
�����F ![]()
���ı���BDFE������
��FD=DB
���ݹ��ɶ����ã� ![]()
�����ã� ![]() =0��
=0��
��ã� ![]() ��
�� ![]()
��F ![]() ��
�� ![]()
II������D��ֱ��AC��ʱ
��D ![]() �����F
�����F ![]()
���ı���BFDE�����Σ�
��FD=FB��
���ݹ��ɶ����ã� ![]()
�����ã� ![]() ��
��
��ã� ![]() (��ȥ)��
(��ȥ)�� ![]()
��F ![]() ��
��
������������F������ֱ�Ϊ�� ![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() .
.
����������1���ɽ�������ķֱ���������߿ɽ��������������ʽ�����⣻��2������ת�ɵ�DG=DB����ΪD��BC�е㣬����DB= ![]() BC����DB�ij�����D�����꣬��ΪG�ڶԳ����ϵĵ㣬�������Ϊ
BC����DB�ij�����D�����꣬��ΪG�ڶԳ����ϵĵ㣬�������Ϊ ![]() ���ɹ��ɶ������췽�̣����G�������ꣻ��3���������ۣ�BE��x���ϣ����Ե�BEΪ�Խ�����ʱ����FDҲΪ�Խ��ߣ����ǻ���ƽ���Ҵ�ֱ������F�ڶԳ����ϣ�DҲ�ڶԳ����ϣ����Ե�D��F����x��Գƣ����DΪAC��Գ���Ľ��㣬BC��Գ���Ľ��㣬�����D���ɣ���BEΪ��ʱ�����ݶԱ�ƽ�пɵñ���DF//BE����D��F����������ȣ���D��BC��ʱ�������D�����꣬�Ӷ��ɵõ�F��������FD=DB�����췽�̽��D�����꣬F������;����D��AC��ʱ��ͬ��.
���ɹ��ɶ������췽�̣����G�������ꣻ��3���������ۣ�BE��x���ϣ����Ե�BEΪ�Խ�����ʱ����FDҲΪ�Խ��ߣ����ǻ���ƽ���Ҵ�ֱ������F�ڶԳ����ϣ�DҲ�ڶԳ����ϣ����Ե�D��F����x��Գƣ����DΪAC��Գ���Ľ��㣬BC��Գ���Ľ��㣬�����D���ɣ���BEΪ��ʱ�����ݶԱ�ƽ�пɵñ���DF//BE����D��F����������ȣ���D��BC��ʱ�������D�����꣬�Ӷ��ɵõ�F��������FD=DB�����췽�̽��D�����꣬F������;����D��AC��ʱ��ͬ��.
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�����Ŀ��ijУ�ڼ��С����������ļ�ֵ�ۡ��ݽ������У�������ǰ20����ѡ�ֵ��ۺϷ���m���з���ͳ�ƣ���������ʾ��
��� | ���� | Ƶ�� |
һ | 6��m��7 | 2 |
�� | 7��m��8 | 7 |
�� | 8��m��9 | a |
�� | 9��m��10 | 2 |

��1����a��ֵ��
��2����������ͼ���������������8��m��9������Ӧ������ͼ��Բ�ĽǴ�С��
��3�����ڵ�һ���ڵ�����ѡ�ּ�Ϊ��A1��A2 �� �ڵ������ڵ�����ѡ�ּ�Ϊ��B1��B2 �� �ӵ�һ��͵����������ѡȡ2��ѡ�ֽ��е�����̸�����һ��������1��ѡ�ֱ�ѡ�еĸ��ʣ�����״ͼ���б����г����п��ܽ������