题目内容
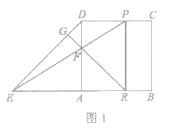
【题目】如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
【答案】
(1)
证明:在□ABCD中,
∵AC与BD相交于点O,
∴OA=OC,AB∥CD,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△OAE≌△OCF,∴OE=OF.
(2)
解:∵△OAE≌△OCF,
∴AE=CF,
∴BE+CF=AB=6,
又∵EF=2OE=4,
∴四边形BCFE的周长=BE+CF+EF+ BC=6+4+5=15(cm)
【解析】(1)由平行四边形的性质可得OA=OC , AB∥CD , ∠OAE=∠OCF , ∠OEA=∠OFC , 则可证明△OAE≌△OCF , 则OE=OF;(2)EF=2OE=4,BC已知,由(1)可得BE+CF=BE+AE=AB.

练习册系列答案
相关题目
【题目】某校计划组织学生到市影剧院观看大型感恩歌舞剧,为了解学生如何去影剧院的问题,学校随机抽取部分学生进行调查,并将调查结果制成了表格、条形统计图和扇形统计图(均不完整). 
(1)此次共调查了多少位学生?
(2)将表格填充完整;
步行 | 骑自行车 | 坐公共汽车 | 其他 |
50 |
(3)将条形统计图补充完整.