题目内容
【题目】（10分）荆州素有“鱼米之乡”的美称，某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售，按计划20辆汽车都要装运，每辆汽车只能装运同一种鱼，且必须装满，根据下表提供的信息，解答以下问题：
（1）设装运鲢鱼的车辆为x辆，装运草鱼的车辆为y辆，求y与x之间的函数关系式；
（2）如果装运每种鱼的车辆都不少于2辆，那么怎样安排车辆能使此次销售获利最大？并求出最大利润．
【答案】（1）y=﹣3x+20；（2）装运鲢鱼的车辆为2辆，装运草鱼的车辆为14辆，装运青鱼的车辆为4辆时获利最大，最大利润为33．2万元．
【解析】试题（1）设装运鲢鱼的车辆为x辆，装运草鱼的车辆为y辆，则由（20﹣x﹣y）辆汽车装运青鱼，根据题意建立等式就可以求出结论；
（2）根据建立不等装运每种鱼的车辆都不少于2辆，列出不等式组求出x的范围，设此次销售所获利润为w元，w=﹣1．4x+36，再利用一次函数的性质即可解答．
试题解析：（1）设装运鲢鱼的车辆为x辆，装运草鱼的车辆为y辆，则由（20﹣x﹣y）辆汽车装运青鱼，由题意，得：8x+6y+5（20﹣x﹣y）=120，∴y=﹣3x+20．
答：y与x的函数关系式为y=﹣3x+20；
（2），根据题意，得：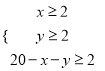 
，∴
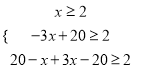，解得：2≤x≤6，
设此次销售所获利润为w元，w=0．25x×8+0．3（﹣3x+20）×6+0．2（20﹣x+3x﹣20）×5=﹣1．4x+36，∵k=﹣1．4＜0，∴w随x的增大而减小．∴当x=2时，w取最大值，最大值为：﹣1．4×2+36=33．2（万元）．
答：装运鲢鱼的车辆为2辆，装运草鱼的车辆为14辆，装运青鱼的车辆为4辆时获利最大，最大利润为33．2万元．
练习册系列答案
相关题目
