题目内容
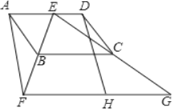
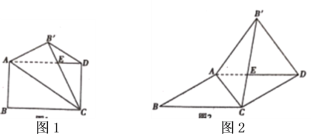
【题目】如图所示,在![]() 和
和![]() 中给出4个论断:①
中给出4个论断:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,
,![]() ;现将4个论断分别粘贴在四个学生的后背上,进行如下游戏:其中三个学生站在讲台的左边,另一个学生站在讲台的右边,要求以三个学生后背上的部分论断作为题设,另一个学生后背上的论断作为结论,使之成为一个真命题或题目,这个游戏可进行几轮?并对其中的一种情况进行证明.
;现将4个论断分别粘贴在四个学生的后背上,进行如下游戏:其中三个学生站在讲台的左边,另一个学生站在讲台的右边,要求以三个学生后背上的部分论断作为题设,另一个学生后背上的论断作为结论,使之成为一个真命题或题目,这个游戏可进行几轮?并对其中的一种情况进行证明.
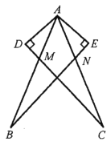
【答案】可进行3轮;②③④→①;①②④→③;①③④→②,证明详见解析.
【解析】
仔细阅题目,要求出游戏可进行的轮数,即要判断出符合题设条件的所有命题中正确命题的个数,结合题中的4个论断,试着写出符合题意的所有命题;对于命题②③④→①可根据ASA即可证明两个三角形全等,从而得出推理.
可进行3轮;②③④→①;①②④→③;①③④→②.
对于命题②③④→①:
已知![]() ,
,![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
证明:∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,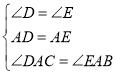
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,为迎接第
个世界读书日,为迎接第![]() 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按![]() 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.