题目内容
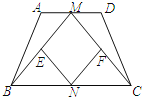
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
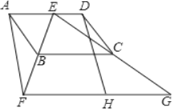
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=60°,∠DCE=20°,求∠CBE的度数.
【答案】(1)证明见解析;
(2)∠CBE=70°.
【解析】
(1)证明AD∥BC,AD=BC,FH∥BC,FH=BC;
(2)∠CBE是等腰△CBE的底角,求出顶角∠ECD即可.
(1)证明:∵BF=BE,CG=CE,
∴BC∥![]() FG,BC=
FG,BC=![]() FG
FG
又∵H是FG的中点,
∴FH∥![]() FG,FH=
FG,FH=![]() FG,
FG,
∴BC∥FH,且BC=FH,
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AD∥FH,
∴四边形AFHD是平行四边形;
(2)∵四边形ABCD是平行四边形,∠BAE=60°,
∴∠BAE=∠DCB=60°,
又∵∠DCE=20°,
∴∠ECB=∠DCB-∠DCE=60°-20°=40°,
∵CE=CB,
∴∠CBE=∠BEC=![]() (180°-∠ECB)=
(180°-∠ECB)=![]() (180°-40°)=70°.
(180°-40°)=70°.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目